Basic Concepts of Prob. and Stats.
NRES 710
Fall 2022
Overview of basic concepts of probability and statistics
We use probability and statistics to make inferences from data!
For example, say I asked you: can people with last names beginning A-M jump higher than those with last names beginning N-Z?
As a scientist, what would we do?
We would want to identify, and then sample, the population of interest! The process of making inferences about the world based on sample data is called statistics!
Statistics
The figure below illustrates the basic concepts of statistics (we’ve already seen this). The bold line separates the unseen population of interest (left) from the observed sample (right):
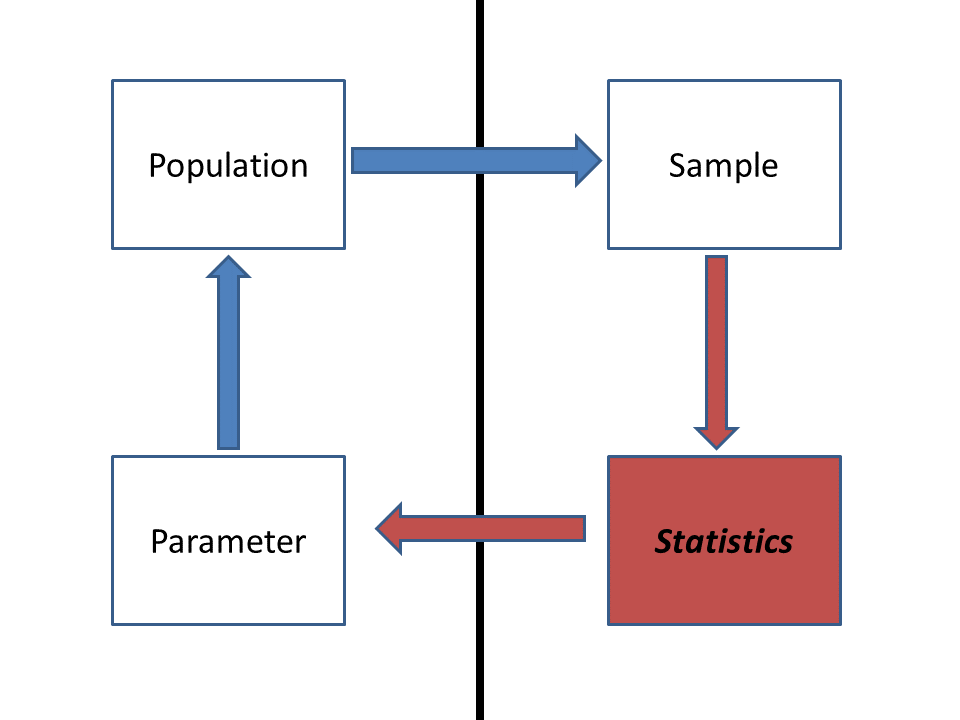
Statistics is about using the things we can observe (the sample) to say something meaningful about the things we can’t observe (the population).
Q: what is the population in the above
example?
Q what is the parameter in the above example?
Q what is the sample in the above example?
Q what is the ‘statistic’ in the above example?
Population: ???
Parameter: ???
Sample: ???
Statistic: ???
For statistical inference to make sense, we must make several assumptions about the sample (i.e., that the sample is representative of the population).
Classical statistics often involves comparing a statistic computed from the data (the “signal”) with a (usually theoretical) ‘sampling distribution’ to quantify the “noise” or sampling error and ultimately determine whether or not we can say anything meaningful about the unseen parameter.
Where does probability come in? Well, samples are random- all statistics are derived from random sampling processes.
How can we tease apart signal from noise- i.e., determine that our result is meaningful and not simply an artifact of random sampling?
Probability helps us to quantify uncertainty and make sense of processes that come out different every time -like random sampling!
Specifically, we use a special type of probability distribution known as a “sampling distribution” to quantify how much noise to expect from our random sampling process (this is also the topic of our next lecture).
Sampling distributions
Q: what is the probability of getting four heads out of 4 coin flips from a fair coin?
We assume that heads or tails are equally likely outcomes of a single coin flip (fair coin) and that the four flips are completely independent.
How many possible outcomes are there?
TTTT
TTTH
TTHT
TTHH
THTT
THTH
THHT
THHH
HTTT
HTTH
HTHT
HTHH
HHTT
HHTH
HHHT
HHHH
Assuming a ‘fair’ coin each of these outcomes/sequences is equally likely!
What is the probability (expected frequency) of all four coin flips coming out heads?
If you get four heads in a row, are you surprised enough by that outcome to reject the assumption that the coin is ‘fair’? What about if you got 100 heads in a row?
Q What is the probability of getting at least three of the same face (heads or tails) out of 4 coin flips? Would this cause you to reject the fairness of the coin?
The distribution of possible outcomes from your sampling process (often under strict assumptions- like assuming a fair coin) is a sampling distribution.
The notion that the coin is a fair coin is an example of a null hypothesis…
Null hypotheses and statistical tests
The null hypothesis is the notion that the particular signal you are looking for is entirely absent in the population of interest.
Under the null hypothesis, any hypothetical random samples you collect might have some apparent signal, but that apparent signal is just a meaningless artifact of random sampling, and not representative of the population (after all, the signal is completely absent in the population under the null hypothesis).
Q what is the null hypothesis for the jump-height example?
P values
The p value is a key concept of frequentist statistics, but one that is often misinterpreted and misunderstood.
The p value only has meaning in the context of the null hypothesis- that is, in a world where the null hypothesis is true. I will sometimes refer to this as the “null universe”.
The p value answers the question: “what’s the probability that my observed result (or one even more”extreme” –i.e., with even more “signal”) could have occurred by chance given the null hypothesis is true?”
The lower the p-value, the more surprised you will be that your observed data could be a meaningless result of random chance alone AND the more likely you might be to reject the null hypothesis!
Q: What does a p-value tell you about your alternative hypothesis?
Aside: extremeness
The p value definition is accompanied by the word “extreme”: the probability of observing a result at least as extreme as your observed result, given the null hypothesis is true.
A result ‘at least as extreme as your observed result’ means a sample dataset that has at least as much “signal” as your observed data.
For example:
Sample size: 20, 10 with names between A and M and 10 with
names between N and Z.
Observed result: mean jump-height for A-M is 0.2 cm greater
than mean height for N-Z
Q Would you be comfortable rejecting the null
hypothesis if random sampling under the null hypothesis could produce a
result as or more extreme approximately 20% of the time (p = 0.2)?
Statistical tests: rejecting the null!
A p value is not in itself a statistical test. A p-value is a probability, which can take values between 0 and 1. It doesn’t in itself tell you whether or not you should reject the null hypothesis!
We reject the null hypothesis if the p value falls below a threshold - this threshold is known as alpha, or \(\alpha\)).
\(\alpha\) is usually set by the researcher. It is arbitrary and has to do with your risk tolerance as a researcher.
How comfortable are you with rejecting the null if there is a 10% chance that your result could have been generated under the null?
How comfortable are you with rejecting the null if there is a 1% chance that your result could have been generated under the null?
Fisher proposed \(\alpha =0.05\) as striking a nice balance between mistakenly rejecting a true null hypothesis (Type 1 error), and failing to reject a false null hypothesis (a Type 2 error). This cutoff value was NEVER intended to be a fixed value to be applied unthinkingly!!!
Example: Fisher’s cups of tea:
A Woman claimed she could tell if milk was added to a cup of tea first or last.
Fisher suggested we give her 8 seemingly identical cups of tea at once, 4 with milk first and 4 with tea first. The woman is asked to identify the four cups that were poured with milk first, given the 8 cups are presented to the woman in a randomized order.
There are 70 possible ways of choosing four cups out of 8. The probability of getting all of them right by random chance (assuming the null is true) would be 1/70 = 0.014 = 1.4%. That would be kinda surprising, right? So if the lady selected all four cups correctly, are we surprised enough to reject the null?
Q: How would you state the null hypothesis in words?
Q: If we decide to reject the null, what do we now believe about our tea-taster?
Q: If we fail to reject the null, what do we now believe about our tea-taster? More specifically, do we now know she is a fraud?
Here are the possibilities (X=incorrect id, O=correct id), which under the null hypothesis are equally likely (since the lady can’t actually tell the difference under the null hypothesis). Let’s assume cups 5-8 are milk first and 1-4 are milk last. The number of correct choices is in parentheses.
X1/X2/X3/X4 (0) X1/X3/X4/O5 (1) X1/X4/O7/O8 (2) X2/X4/O5/O6 (2)
X3/X4/O7/O8 (2)
X1/X2/X3/O5 (1) X1/X3/X4/O6 (1) X1/O5/O6/O7 (3) X2/X4/O5/O7 (2)
X3/O5/O6/O7 (3)
X1/X2/X3/O6 (1) X1/X3/X4/O7 (1) X1/O5/O6/O8 (3) X2/X4/O5/O8 (2)
X3/O5/O6/O8 (3)
X1/X2/X3/O7 (1) X1/X3/X4/O8 (1) X1/O5/O7/O8 (3) X2/X4/O6/O7 (2)
X3/O5/O7/O8 (3)
X1/X2/X3/O8 (1) X1/X3/O5/O6 (2) X1/O6/O7/O8 (3) X2/X4/O6/O8 (2)
X3/O6/O7/O8 (3)
X1/X2/X4/O5 (1) X1/X3/O5/O7 (2) X2/X3/X4/O5 (1) X2/X4/O7/O8 (2)
X4/O5/O6/O7 (3)
X1/X2/X4/O6 (1) X1/X3/O5/O8 (2) X2/X3/X4/O6 (1) X2/O5/O6/O7 (3)
X4/O5/O6/O8 (3)
X1/X2/X4/O7 (1) X1/X3/O6/O7 (2) X2/X3/X4/O7 (1) X2/O5/O6/O8 (3)
X4/O5/O7/O8 (3)
X1/X2/X4/O8 (1) X1/X3/O6/O8 (2) X2/X3/X4/O8 (1) X2/O5/O7/O8 (3)
X4/O6/O7/O8 (3)
X1/X2/O5/O6 (2) X1/X3/O7/O8 (2) X2/X3/O5/O6 (2) X2/O6/O7/O8 (3)
O5/O6/O7/O8 (4)
X1/X2/O5/O7 (2) X1/X4/O5/O6 (2) X2/X3/O5/O7 (2) X3/X4/O5/O6 (2)
X1/X2/O5/O8 (2) X1/X4/O5/O7 (2) X2/X3/O5/O8 (2) X3/X4/O5/O7 (2)
X1/X2/O6/O7 (2) X1/X4/O5/O8 (2) X2/X3/O6/O7 (2) X3/X4/O5/O8 (2)
X1/X2/O6/O8 (2) X1/X4/O6/O7 (2) X2/X3/O6/O8 (2) X3/X4/O6/O7 (2)
X1/X2/O7/O8 (2) X1/X4/O6/O8 (2) X2/X3/O7/O8 (2) X3/X4/O6/O8 (2)
Q what if the lady selected 3 of 4 correctly? [there are 17 ways of getting at least three of the four correct out of 70 total combinations]. Would you be surprised enough to reject the null hypothesis. Is it possible that you (and the lady) are living in the null universe? How surprised would you have to be to reject the null and admit that she can tell the difference?
ASIDE: the test above is called ‘Fisher’s exact test’ because it literally enumerates all the possible outcomes to compute the exact probability of observing any particular outcome under the null hypothesis. Most tests we will use in this class are (necessarily) approximations that rely on certain assumptions that may or not be met in practice. Fisher’s exact test assumes that all observations are independent, but otherwise makes no additional assumptions.
Statistics Terminology: Type 1 and Type 2 errors
A type 1 error is mistakenly rejecting the null hypothesis (false positive).
The type 1 error rate (alpha) is the probability of committing a false positive error- given the null is true, how often would you reject the null?
A type 2 error is mistakenly failing to reject a false null hypothesis (you are not living in the null universe but you fail to acknowledge it!).
The type 2 error rate is called Beta, or \(\beta\), and is the probability of fail to reject the null assuming the null is false.
Q what would it mean to set the Beta level? Why do
we set alpha rather than beta?
A there is only one universe in which the null
hypothesis is true. There are infinite ways in which the null hypothesis
could be false. It only makes sense to fix the alpha level…
Finally Power is defined as the probability of correctly rejecting an incorrect null hypothesis. Power is simply defined as \(1-\beta\)!
Power is influenced by sample size (amount of information at your disposal) and effect size (the degree to which the null is not true!), among other things. A Power analysis is an attempt to see how much power you have to detect a true signal under a given sampling design.
