For those wishing to follow along with the R-based demo in class, click here for the companion R script for this lecture.

In the previous two lectures, we have discussed model-based inference using likelihood functions in a frequentist framework. Specifically, we have constructed likelihood functions with one or more free parameters and then used numerical optimization to find the maximum-likelihood estimate (MLE). Parameter uncertainty was accommodated by assessing the curvature of the likelihood surface in the vicinity of the MLE (e.g., using the ‘rule of 2’ and the concept of the likelihood profile).

Today we will start discussing Bayesian inference, which is less of a departure from these previous topics than you might think.

Bayesian inference also requires us to develop likelihood functions that describe our hypotheses about how our data were generated.

Bayesian methods also use the curvature of the likelihood surface to make inference about parameter uncertainty.

The difference is that we are no longer interested in the maximum likelihood estimate (MLE) and the properties of maximum likelihood estimators. Instead, we’re interested in using the likelihood function to update our degree of belief about all possible parameter values. Effectively, we want to obtain a joint probability distribution (called the joint posterior distribution) that reflects the probability of any given set of parameters being the true parameter value.

Remember, Bayesian inference allows us to represent parameter uncertainty as probability distributions, so our the parameters of interest are no longer fixed but unknown values (points), they are sets of potential values, each with an associated probability!

Play with binomial/beta (conjugate prior)

Estimating the probability of an event using a binomial distribution is one of the simplest likelihood-based problems, so it provides a good starting point!

Let’s imagine we know N (N, the number of independent trials, is fixed), but we want to estimate p (the probability of an event occurring). For now, we will assume we have no prior information about p, such that any value of p is equally likely.

Set the prior

To set the prior, let’s assume p follows a uniform distribution between 0 and 1:

# Bayesian analysis example using Binomial distribution  -----------------------

# first visualize the "prior" for the probability *p* as a uniform distribution

curve(dunif(x),ylim=c(0,2),col="red", ylab = "probability", xlab="parameter \"p\"")

#hist(runif(10000),freq=F,ylim=c(0,2),col="red")

An alternative way to specify this uniform (flat) prior is to use the beta distribution, with both parameters of the distribution (shape1 and shape2) set to 1

# Alternative prior: beta distribution (conjugate prior)

curve(dbeta(x,1,1),ylim=c(0,2),col="red",ylab = "probability", xlab="parameter \"p\"")

#hist(rbeta(10000,1,1),freq=F,ylim=c(0,2),col="red")   # histogram of random numbers from a flat beta distribution

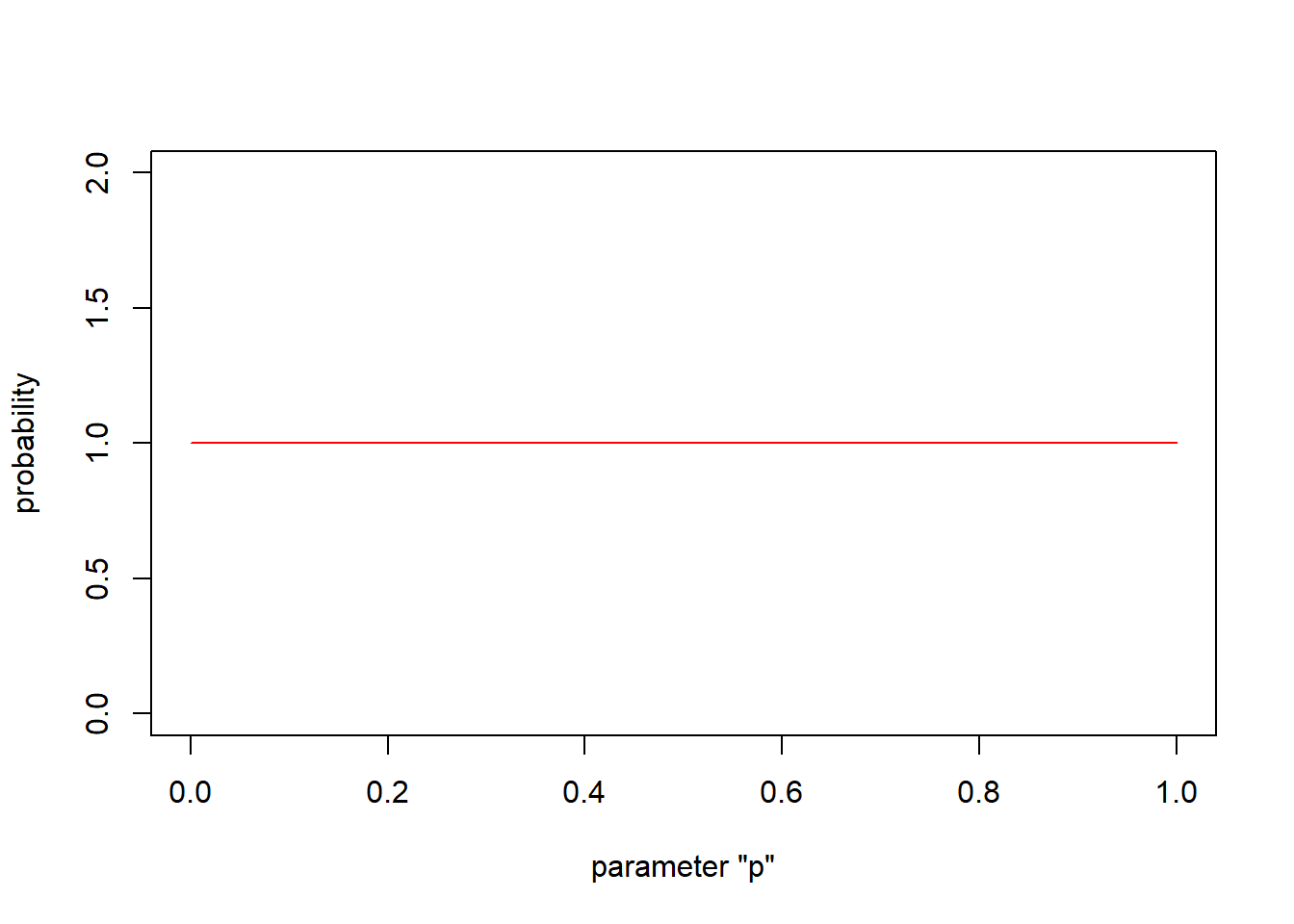
Conjugate prior

Why choose the beta distribution here? The answer is that the beta distribution is the conjugate prior for the p parameter in the binomial distribution. This makes Bayesian estimation easy and straightforward, as we will see!

Definition: conjugate prior

A conjugate prior is a distribution for a parameter that matches the data-generating model: that is, the prior has the same general form as the likelihood function. An important consequence of this is that prior and the posterior distribution can be represented with the same probability distribution (e.g., gamma, beta, normal). We will come back to this!

Worked example

Let’s work through an example. Take the same frog-call survey we have imagined before (a simple problem with binomial data). Recall that a particular site is occupied. After visiting the site 10 times, we detected the frog (heard its call) 3 times out of 10 total visits. We are interested in determining the detection probability.

We know the likelihood of the data across parameter space. So now we have both a prior distribution for our parameter of interest, as well as a likelihood surface.

# frog call example: --------------
#    imagine we detected the frog in 3 of 10 visits to a known-occupied wetland

#    visualize the data likelihood alongside the prior probability

#    recall that the likelihood surface is not a probability distribution (thus, the 2 y axes)

data = 3
param.space <- seq(0,1,by=0.001)
likelihood <- dbinom(data,size=10,prob=param.space)
par(mai=c(1,1,0,1))
curve(dbeta(x,1,1),ylim=c(0,2),col="blue",lty=2,ylab="Probability density (prior)",xlab="parameter (p)")
points(param.space,likelihood,type="l",col="red",lwd=2,lty=2)
axis(4,at=seq(0,.3,length=4),labels = seq(0,0.3,length=4))
mtext("Likelihood (relative plausibility)", side=4, col="red",line=3)

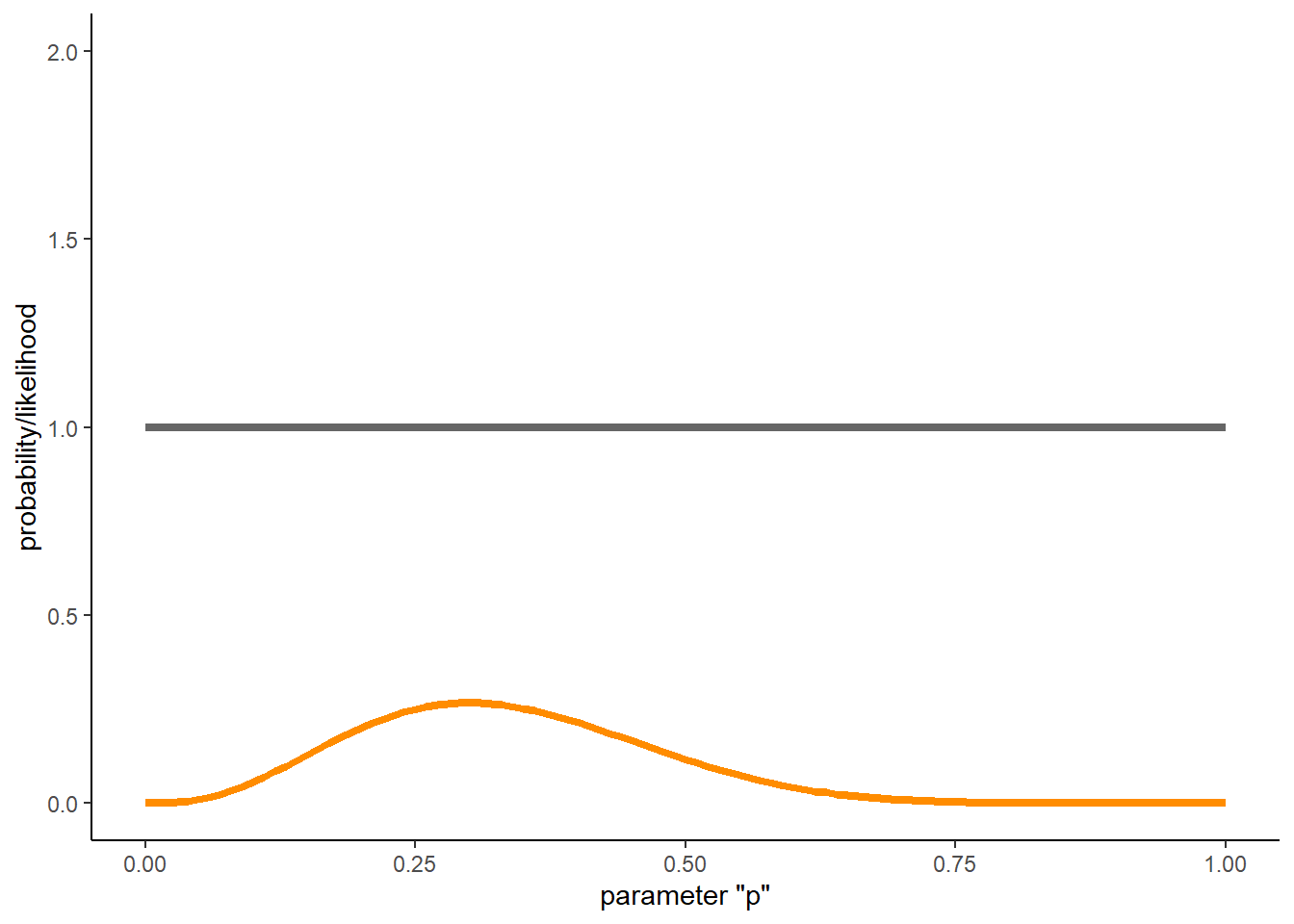
Recall that the likelihood curve is NOT a probability distribution. It does not sum to 1! In Bayesian analyses, we translate the likelihood to a probability distribution using Bayes rule!!

\(Prob(Model|Data) = \frac{Prob(Data|Model)\cdot Prob(Model))}{Prob(Data)}\)

The \(Prob(Data|Model)\) term is the likelihood curve…

The \(Prob(Model)\) term is the prior distribution

BUT… what is the unconditional probability of the data (\(Prob(Data)\))?

Well, it’s the likelihood of the data, summed across all possible parameter values, weighted by the prior. This evaluates to a single number (also known as the “evidence”).

In practical terms, the denominator, \(Prob(Data)\), can be seen as a normalizing constant that effectively converts the numerator \(Prob(Data|Model)\cdot Prob(Model))\) into a true probability distribution.

As always (in this class), let’s do it first by brute force!!

# Brute-force Bayes ----------------------------

####
# prior across parameter space 

prior <- dbeta(param.space,shape1=1,shape2=1)    # flat prior
#prior

####
## Numerator for Bayes rule: weight the data likelihood by the prior

weighted.likelihood <- likelihood*prior      # Numerator for Bayes rule

####
## Denominator for Bayes rule: compute normalization constant

normalization.constant <- sum(weighted.likelihood)   # "evidence" is a single constant number: the sum of the weighted likelihoods!

####
## Posterior!! (numerator/denominator)

posterior <- weighted.likelihood/normalization.constant   # this is Bayes' rule!

#####
## Plot it out!

par(mai=c(1,1,0,1))
plot(param.space,prior,ylim=c(0,5),type="l",lwd=1,lty=2,col="blue",ylab="Probability Density",xlab="param.space")
points(param.space,posterior*length(param.space),type="l",col="blue",lwd=2,lty=1)  # convert posterior probability to probability density
points(param.space,likelihood,type="l",col="red",lwd=1,lty=2)
axis(4,at=seq(0,.3,length=4),labels = seq(0,0.3,length=4))
mtext("Likelihood", side=4, col="red",line=3)

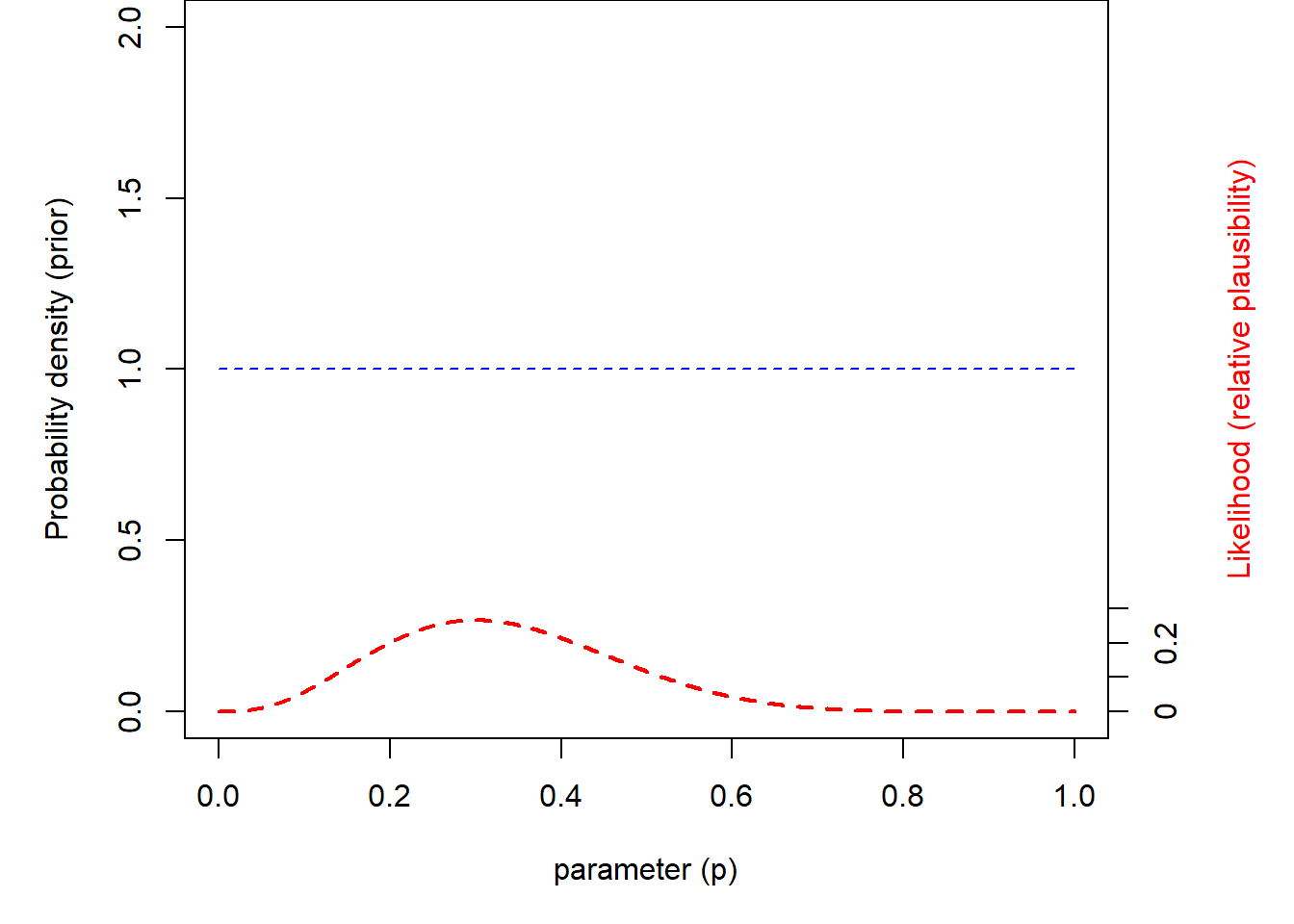
Notice that the shape of the posterior distribution looks a lot like the shape of the likelihood surface. What this says to us is that the prior information has been overwhelmed by the information content of the data (as summarized by the likelihood surface).

Again: recall that the likelihood surface is NOT a probability distribution- it is a way to assess the relative plausibility of the data across parameter space. The prior and the posterior are true probability distributions, and necessarily integrate to 1.

What if we have a more informative prior?

# Try an informative prior!  -------------

prior <- dbeta(param.space,shape1=15,shape2=5)
#prior

## weight the data likelihood by the prior

weighted.likelihood <- likelihood*prior

## compute normalization constant

normalization.constant <- sum(weighted.likelihood)

## Posterior!!

posterior <- weighted.likelihood/normalization.constant

## Plot it out!
par(mai=c(1,1,0,1))
plot(param.space,prior,ylim=c(0,5),type="l",lwd=1,lty=2,col="blue",ylab="Probability Density",xlab="param.space")
points(param.space,posterior*length(param.space),type="l",col="blue",lwd=2,lty=1)
points(param.space,likelihood,type="l",col="red",lwd=1,lty=2)
axis(4,at=seq(0,.3,length=4),labels = seq(0,0.3,length=4))
mtext("Likelihood", side=4, col="red",line=3)

What does this tell us?

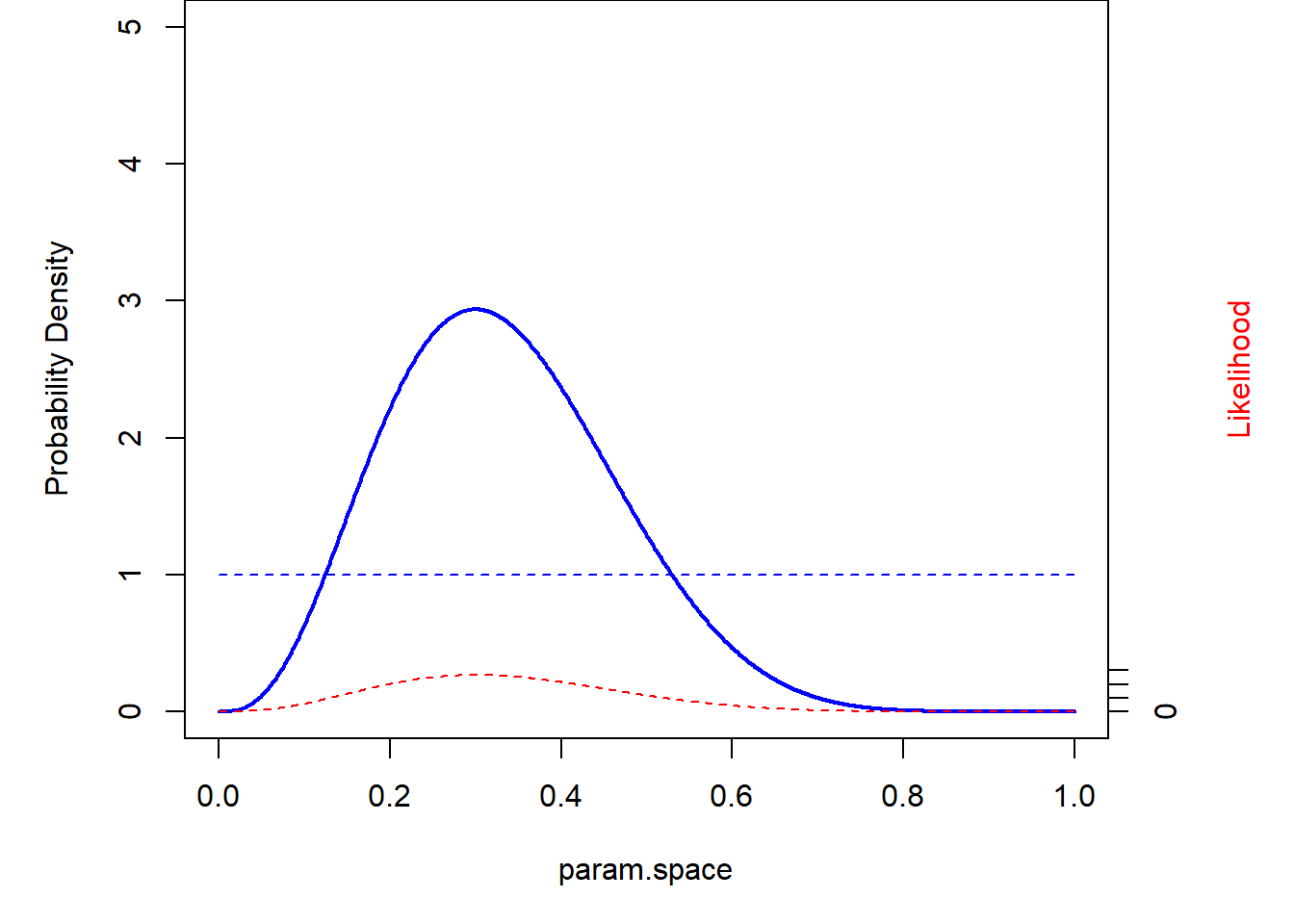
What about if we have more data? Let’s imagine we visited 10 occupied ponds and observed the following data:

3, 1, 6, 2, 3, 2, 6, 1, 3, 3

####
# Collect more data and try again...

moredata <- c(3, 1, 6, 2, 3, 2, 6, 1, 3, 3)

## prior
prior <- dbeta(param.space,shape1=15,shape2=5)

## likelihood
likelihood <- sapply(param.space,function(t) prod(dbinom(moredata,size=10,prob=t)))

## weight the data likelihood by the prior
weighted.likelihood <- likelihood*prior

## compute normalization constant

normalization.constant <- sum(weighted.likelihood)

## Posterior!!

posterior <- weighted.likelihood/normalization.constant

## Plot it out!
par(mai=c(1,1,0,1))
plot(param.space,prior,ylim=c(0,10),type="l",lwd=1,lty=2,col="blue",ylab="Probability Density",xlab="param.space")
points(param.space,posterior*length(param.space),type="l",col="blue",lwd=2,lty=1)
points(param.space,likelihood*1e9,type="l",col="red",lwd=1,lty=2)
axis(4,at=seq(0,6,by=1),labels = seq(0,6e-9,by=1e-9))
mtext("Likelihood", side=4, col="red",line=3)

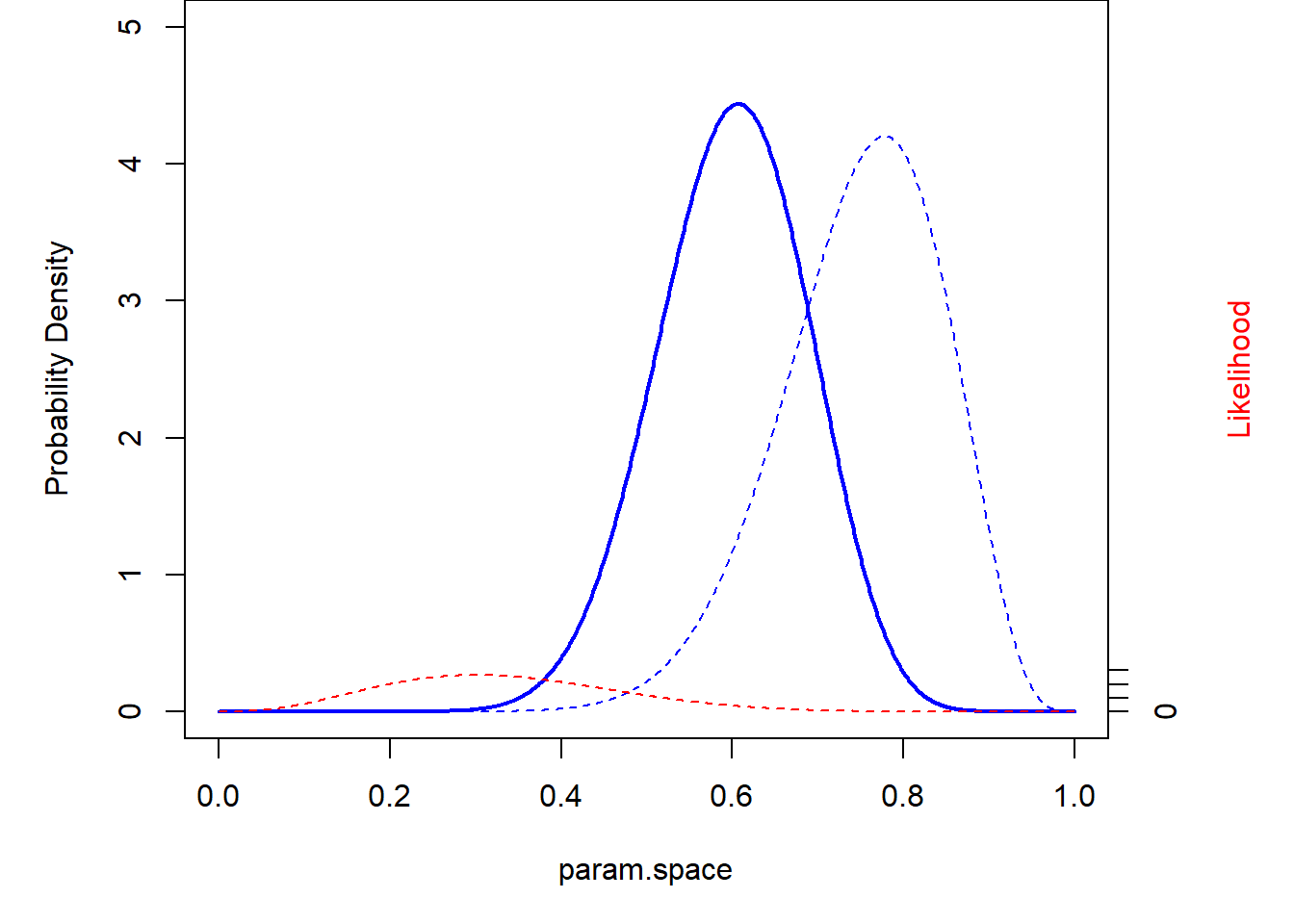
What about a super informative prior??

####
# Try a very informative prior!

likelihood <- dbinom(data,size=10,prob=param.space)
prior <- dbeta(param.space,shape1=150,shape2=50)
#prior

## weight the data likelihood by the prior

weighted.likelihood <- likelihood*prior

## compute normalization constant

normalization.constant <- sum(weighted.likelihood)

## Posterior!!

posterior <- weighted.likelihood/normalization.constant

## Plot it out!
par(mai=c(1,1,0,1))
plot(param.space,prior,ylim=c(0,15),type="l",lwd=1,lty=2,col="blue",ylab="Probability Density",xlab="param.space")
points(param.space,posterior*length(param.space),type="l",col="blue",lwd=2,lty=1)
points(param.space,likelihood*5,type="l",col="red",lwd=1,lty=2)
axis(4,at=seq(0,2,by=0.4),labels = seq(0,0.5,by=.1))
mtext("Likelihood", side=4, col="red",line=3)

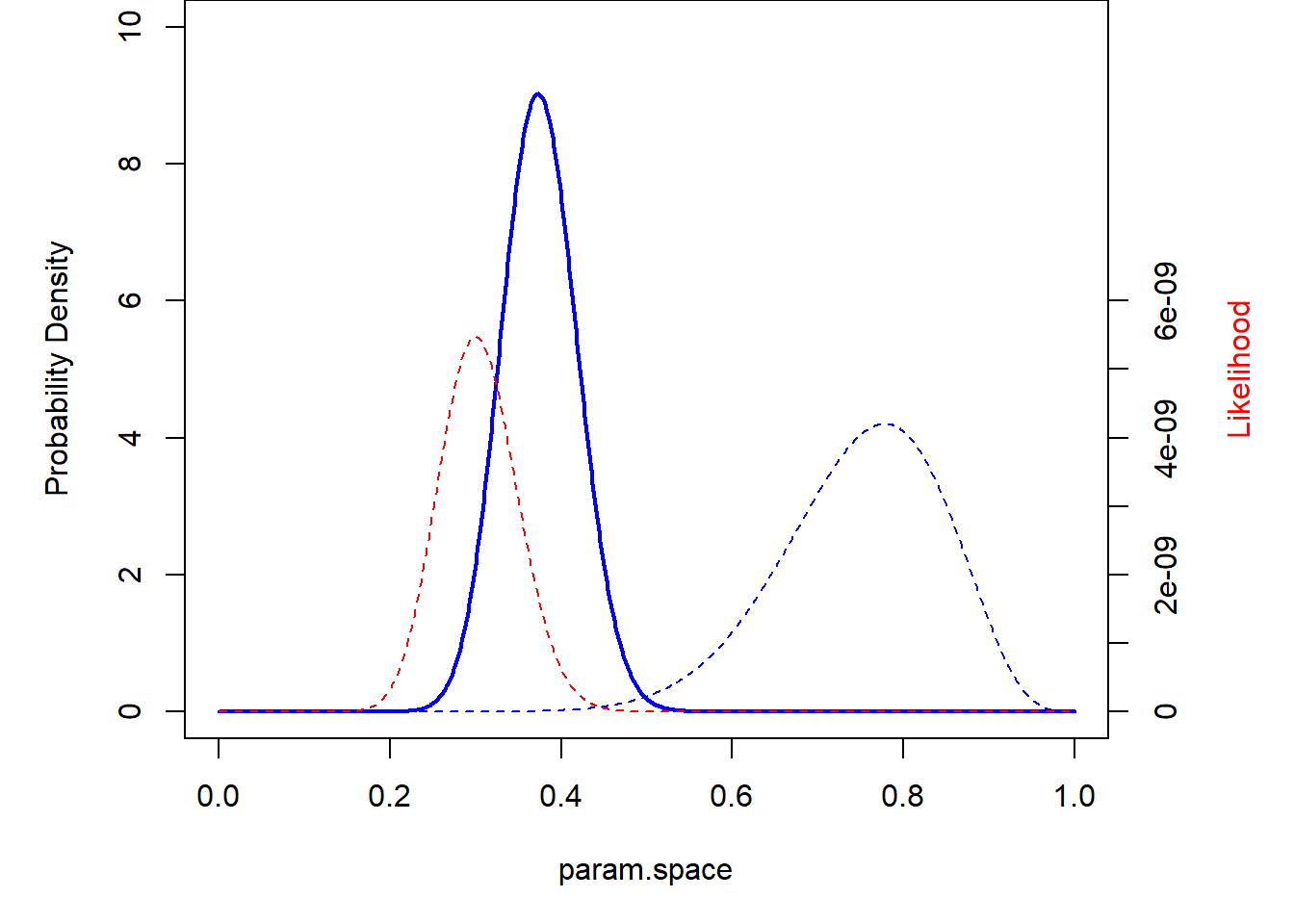
Okay, now let’s do it the more mathematically elegant way! When we work with a conjugate prior, the updating process is easy. The posterior distribution for the p term in the above example can be computed by:

\(Beta(shape1=prior+k,shape2=prior+(N-k))\)

Let’s do the same thing, now using the conjugate prior method…

## Conjugate priors ---------------------------
# Do it again- this time with conjugate priors...

### PRIOR

prior_beta <- c(shape1=1,shape2=1)
curve(dbeta(x,prior_beta['shape1'],prior_beta['shape2']),ylim=c(0,5),ylab="Prob Density",col="blue",lwd=1,lty=2,xlab="param.space")

### POSTERIOR

curve(dbeta(x,prior_beta['shape1']+data,prior_beta['shape2']+(10-data)),ylim=c(0,4),ylab="Prob Density",col="blue",lwd=2,lty=1,xlab="param.space",add=T)

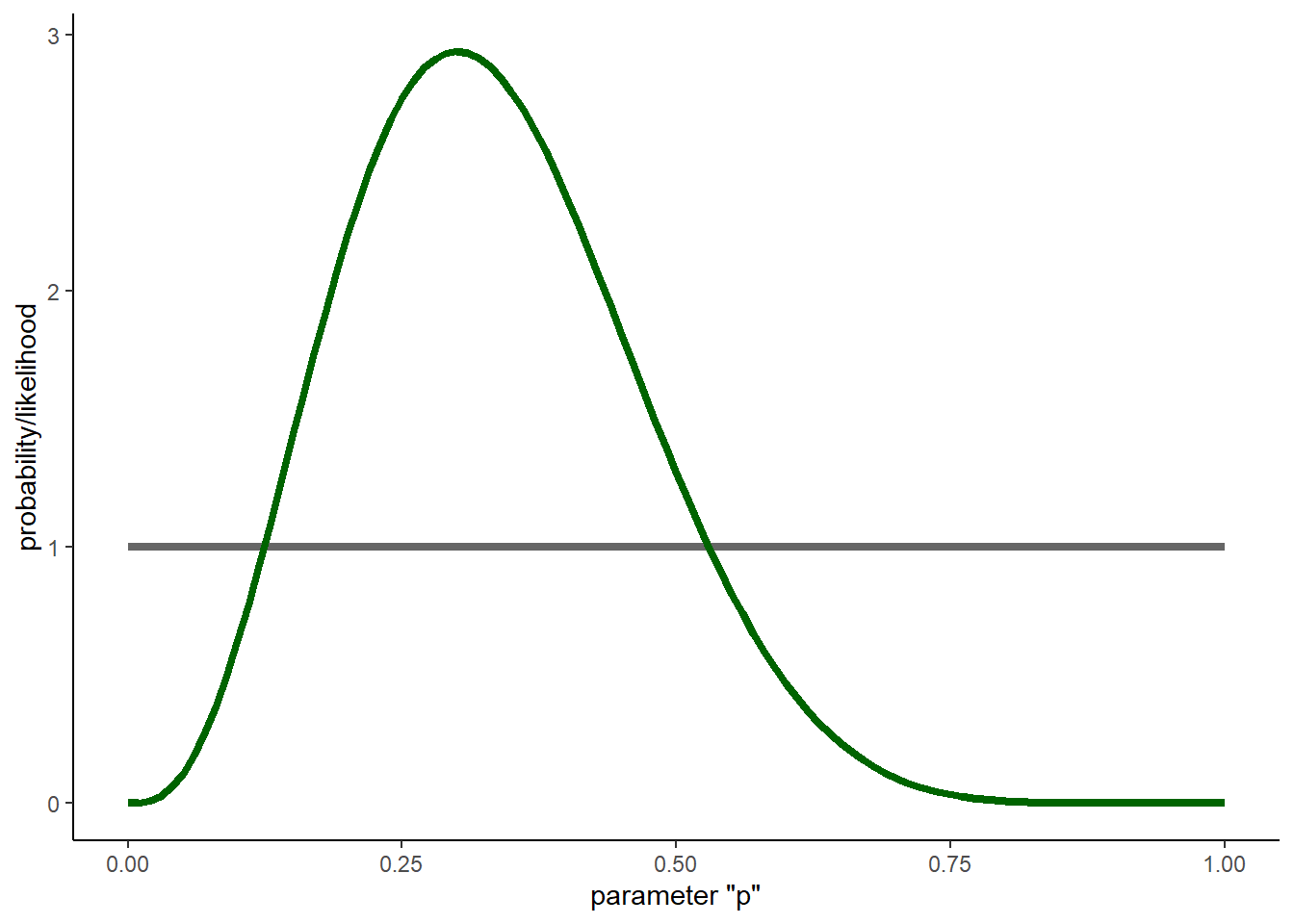
And again, this time with an informative prior!

####
# With informative prior...

### PRIOR
prior_beta <- c(shape1=15,shape2=5)
curve(dbeta(x,prior_beta['shape1'],prior_beta['shape2']),ylim=c(0,5),ylab="Prob Density",col="blue",lwd=1,lty=2,xlab="param.space")


### POSTERIOR

curve(dbeta(x,prior_beta['shape1']+data,prior_beta['shape2']+(10-data)),ylim=c(0,4),ylab="Prob Density",col="blue",lwd=2,lty=1,xlab="param.space",add=T)

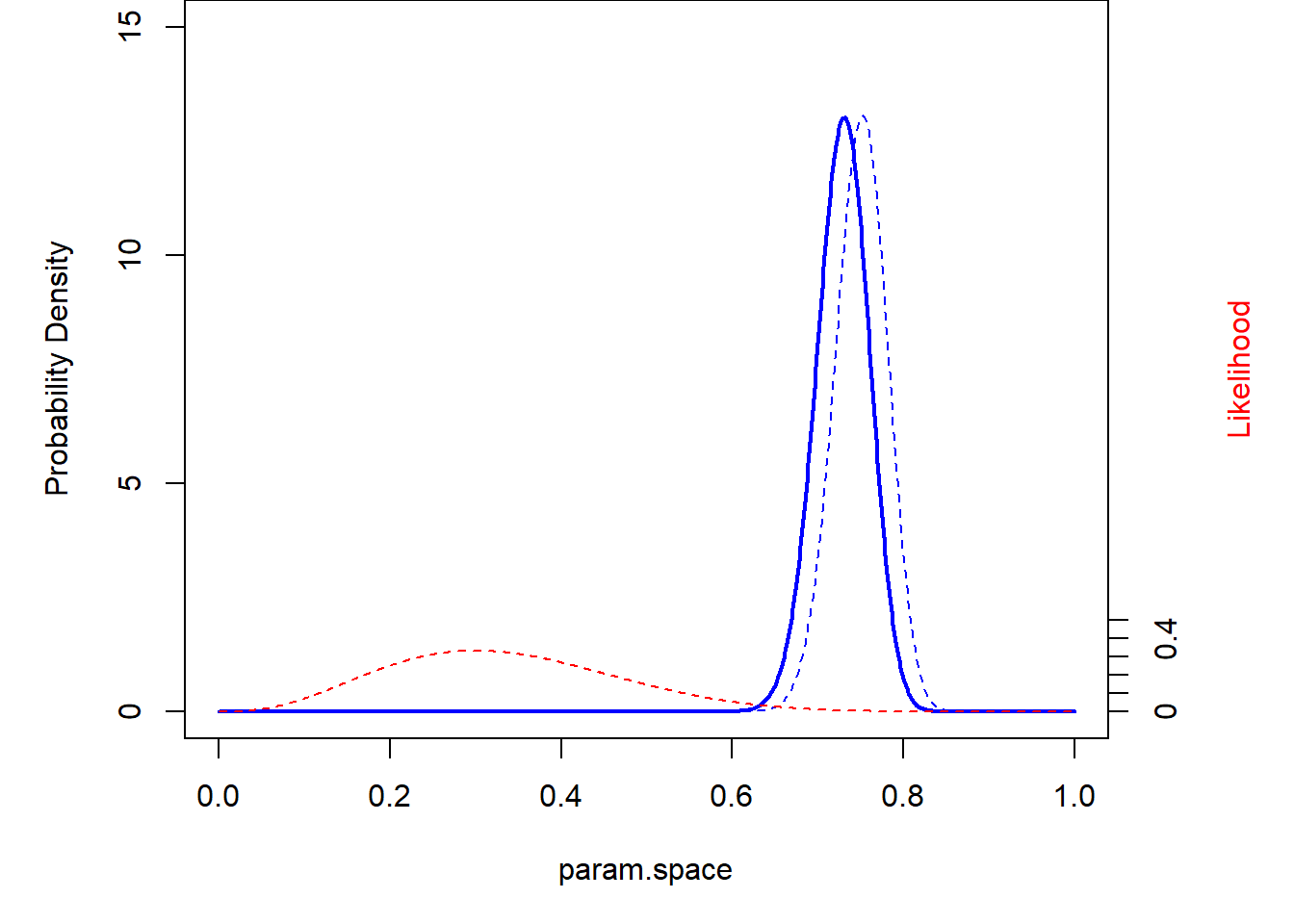
graphics.off()

And the super informative prior??

####
# And with super informative prior...

### PRIOR
prior_beta <- c(shape1=150,shape2=50)
curve(dbeta(x,prior_beta['shape1'],prior_beta['shape2']),ylim=c(0,15),ylab="Prob Density",col="blue",lwd=1,lty=2,xlab="param.space")


### POSTERIOR
curve(dbeta(x,prior_beta['shape1']+data,prior_beta['shape2']+(10-data)),ylim=c(0,15),ylab="Prob Density",col="blue",lwd=2,lty=1,xlab="param.space",add=T)

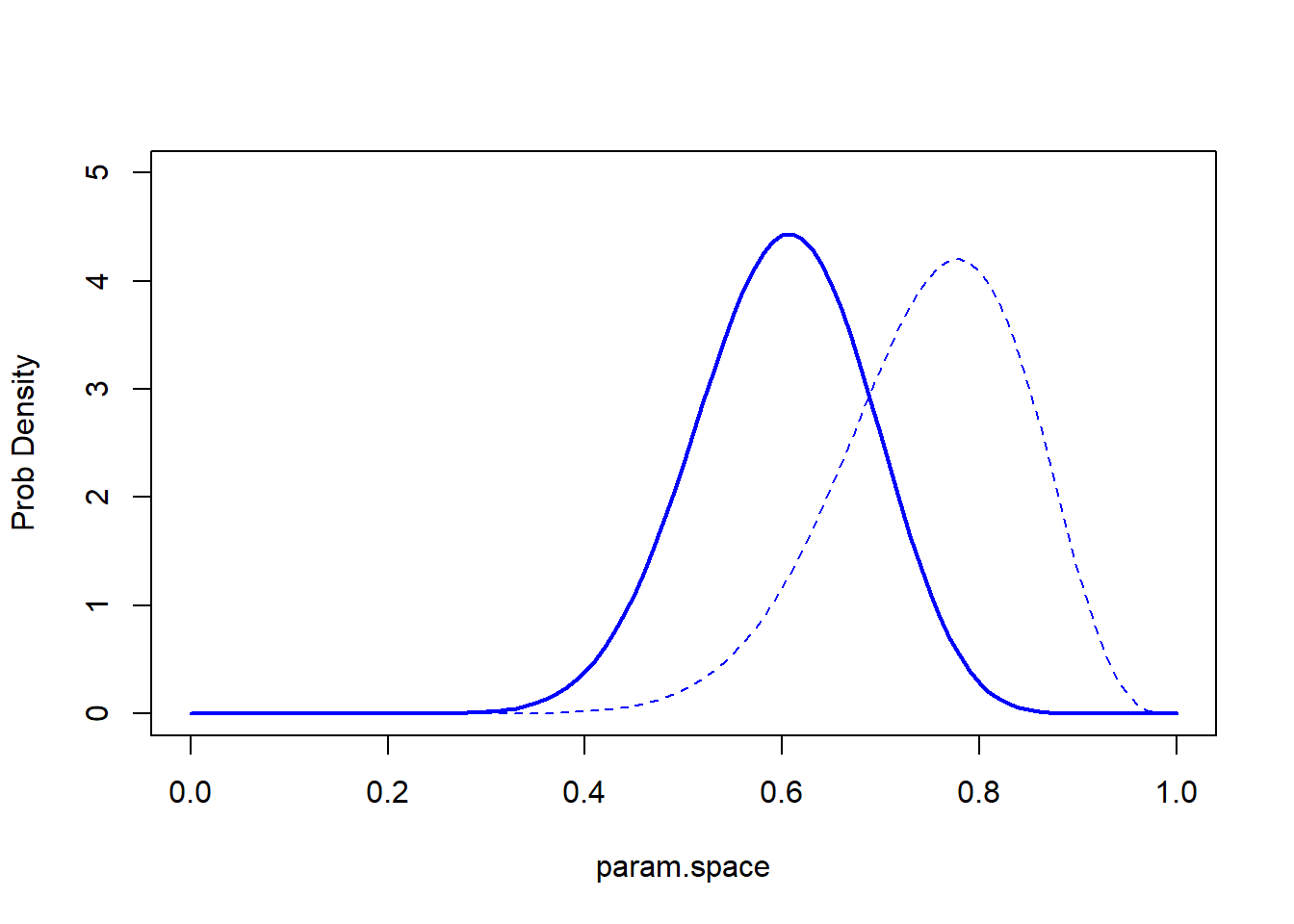
Bayesian point estimate

One of the differences between the MLE and the Bayesian paradigm (although both use likelihood as a way to summarize the information content of the data) is that the point estimate is not usually the maximum (mode) of the posterior distribution (in MLE, we by definition try to find the parameter value that maximizes the likelihood function) but the mean (expected value) or the median of the posterior distribution.

Imagine you had a skewed posterior distribution that looked something like this (this is actually a lognormal distribution):

## Bayesian point estimate -----------------------
# Example: bayesian point estimates can differ markedly from MLE

curve(dlnorm(x,4,1),from=0.001,to=200,ylab="prob density")  # use a lognormal distribution for example of skewed posterior dist...

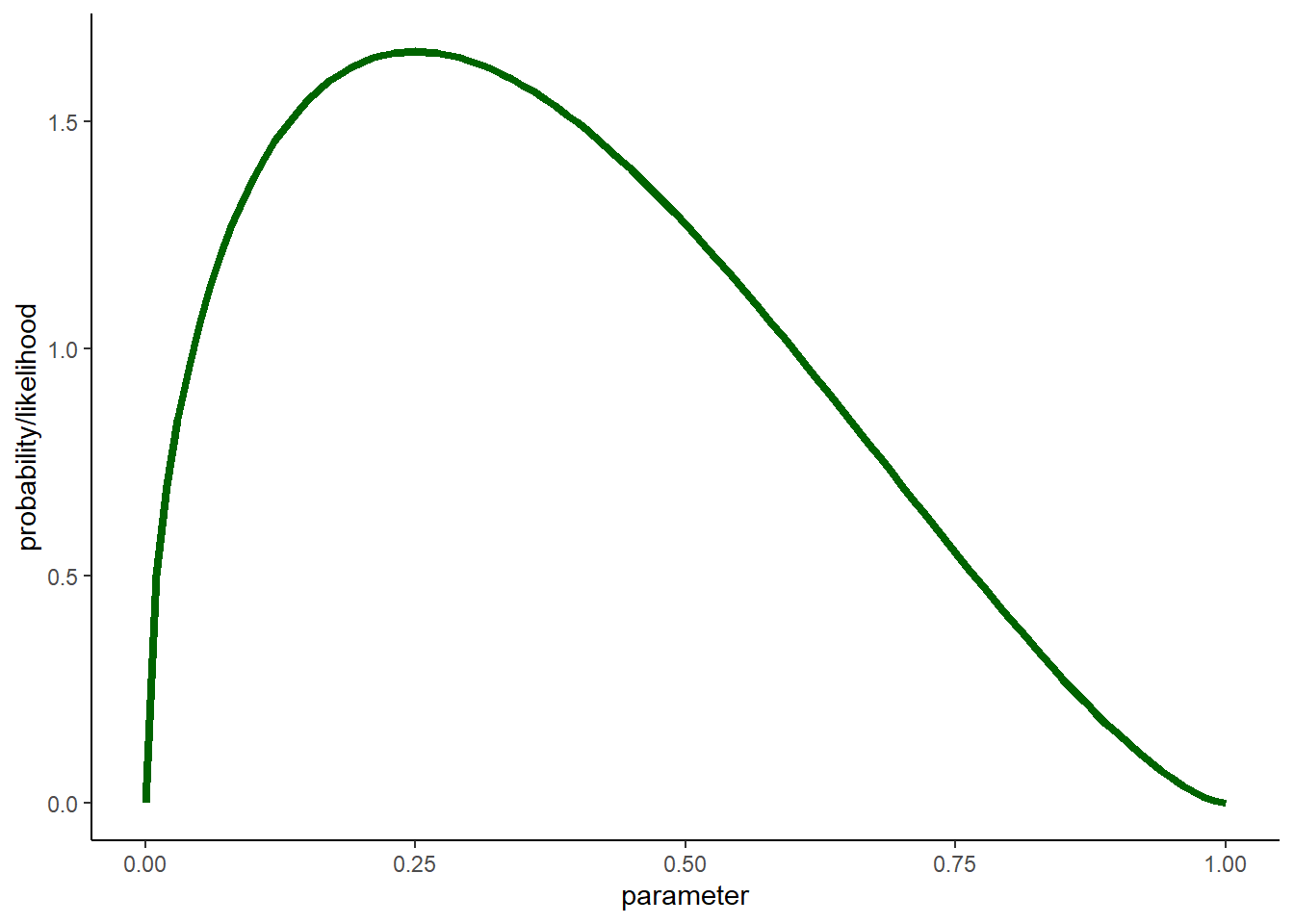
Where is the mode? Where is the mean?

####
# Compute and plot the mean and the mode of the distribution

param.space2 <- seq(0.001,200,length=10000)
skewed.posterior <- dlnorm(param.space2,4,1)
mean <- mean(rlnorm(10000,4,1))
mode <- param.space2[which.max(skewed.posterior)]
plot(param.space2,skewed.posterior,type="l",ylab="prob density")
abline(v=c(mean,mode),col=gray(c(0.5,0.2)),lwd=3,lty=2)   # add to plot

What about for the first worked example? Is there a big difference between the mean and the mode?

####
# Do the same for the frog detection example from above

#graphics.off()
### POSTERIOR
posterior <- dbeta(param.space,1+data,1+(10-data))
mean <- mean(rbeta(10000,1+data,1+(10-data)))
mode <- param.space[which.max(posterior)]
plot(param.space,posterior,type="l",col="blue",lwd=2)
abline(v=c(mean,mode),col=gray(c(0.5,0.2)),lwd=3,lty=2)   # add to plot

Thought question

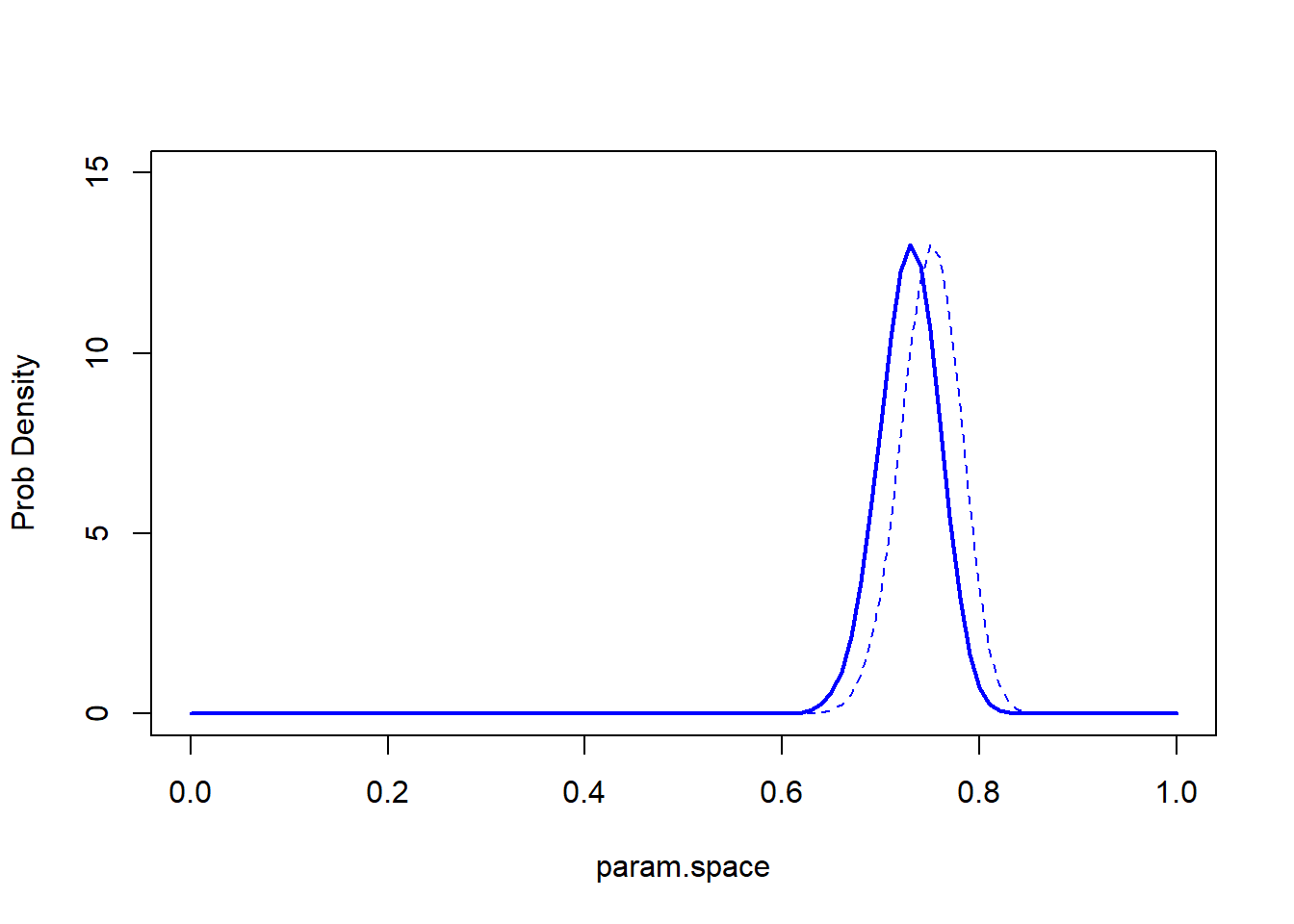
In MLE, we find the parameter value that maximizes the likelihood function. Why don’t we use the mean of the likelihood function in Frequentist statistics? In Bayesian analysis, why don’t we use the mode of the posterior distribution?

Bayesian parameter uncertainty

We often call Bayesian confidence intervals credible intervals to distinguish from their frequentist analog. Bayesian (e.g., 95%) credible intervals can be interpreted in the way you probably have always wanted to interpret frequentist (95%) confidence intervals. It is way more satisfying for many people!

You are 95% sure that the parameter value is between the lower and upper bound!!!

Q: Why can’t we say this in a frequentist framework?

Let’s try this:

####
# A Bayesian confidence interval (95% credible interval)  -------------------

### POSTERIOR

curve(dbeta(x,1+data,1+(10-data)),ylim=c(0,4),ylab="Prob Density",col="blue",lwd=2,lty=1,xlab="param.space")

### CREDIBLE INTERVAL

credible.interval <- qbeta(c(0.025,0.975),1+data,1+(10-data))     # get the credible interval using the quantile method

abline(v=credible.interval,col=gray(0.5),lwd=3,lty=2)   # add to plot

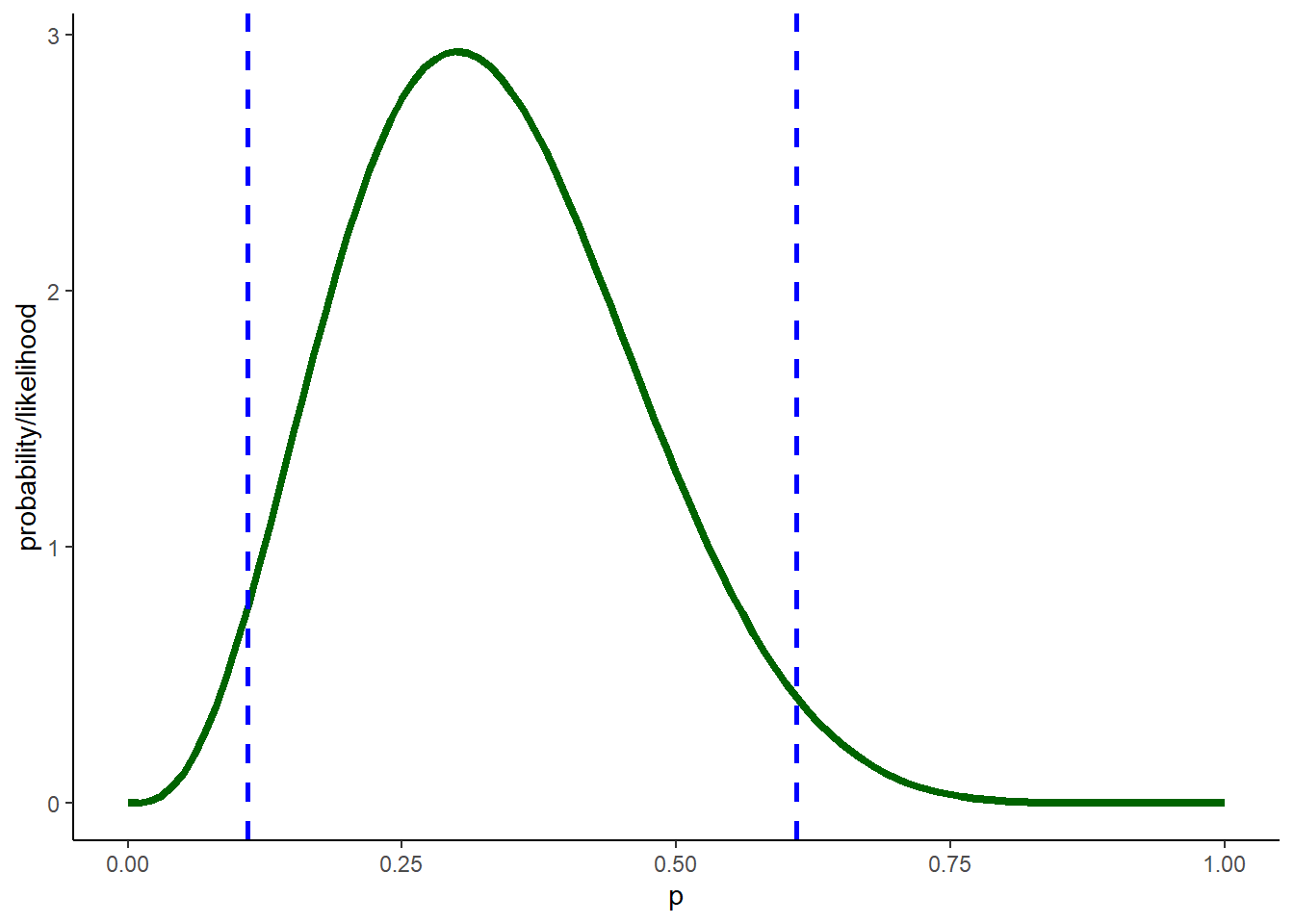
Highest Posterior Density (HPD) intervals

There are many possible Bayesian credible intervals, even assuming we want a 95% CI. That is, there are many intervals that enclose 95% of the posterior distribution. The Highest Posterior Density interval is the one that is the shortest out of all possible intervals. This is the natural choice for a Bayesian CI since it represents the collection of the most likely values for the parameters - every point within the interval is more plausible than any point outside the interval.

NOTE: the HPD can be discontinuous for multimodal posterior distributions!

What if there is no nice easy conjugate prior?

One of the reasons Bayesian analysis was less common historically was that there were no mathematically straightforward ways to do the analysis. There still are not BUT we have fast computers and ingenious computational algorithms. Basically, we can use various forms of more-or-less brute force computation, along with some mathematical tricks, to successfully conduct model-based inference in a Bayesian framework.

Let’s start with the brutest of brute-force methods (not possible in high-dimensional systems):

The brute force method

For continuity we will continue the myxomatosis dataset. Recall that we are estimating the shape and scale (or alternatively, the rate) parameters of the Gamma distribution that describes the virus titer in Australian rabbits for the highest-grade infections.

#### Bayesian analysis without a conjugate prior

# Revisit the Myxomatosis example  --------------------------

library(emdbook)

MyxDat <- MyxoTiter_sum
Myx <- subset(MyxDat,grade==1)
head(Myx)
##   grade day titer
## 1     1   2 5.207
## 2     1   2 5.734
## 3     1   2 6.613
## 4     1   3 5.997
## 5     1   3 6.612
## 6     1   3 6.810

Recall the histogram looks like this:

hist(Myx$titer,freq=FALSE)    # visualize the data, again!

And we are trying to fit a Gamma distribution to these data:

### Error is modeled as gamma distributed

hist(Myx$titer,freq=FALSE)
curve(dgamma(x,shape=40,scale=0.15),add=T,col="red")   # note here we are using scale and not rate...

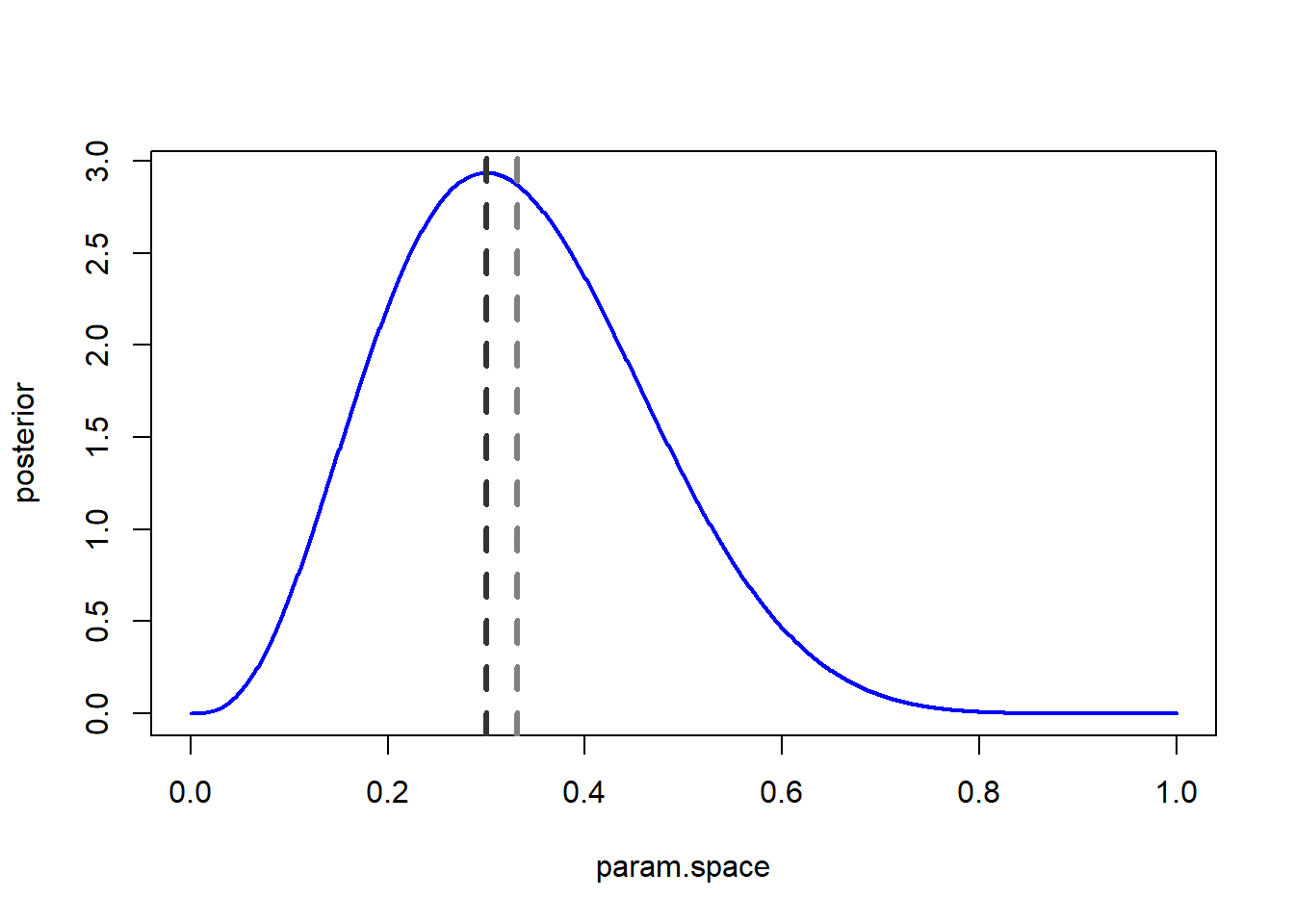
We already have a likelihood function for this problem! Note that we are now looking at raw likelihoods and not log likelihoods!

####
# recall our likelihood function for these data (not on log scale this time!)

GammaLikelihoodFunction <- function(params){
  prod(dgamma(Myx$titer,shape=params['shape'],scale=params['scale']))
}

params <- c(40,0.15) 
names(params) <- c("shape","scale")
params
## shape scale 
## 40.00  0.15
GammaLikelihoodFunction(params)
## [1] 2.906766e-22

And we recall that the 2D likelihood surface looks something like this (looks a bit different without the log transform though!):

# define 2-D parameter space (in real probability scale)!

shapevec <- seq(10,100,by=0.1)   
scalevec <- seq(0.01,0.3,by=0.001)

# define the likelihood surface across this grid within parameter space

likelihood2D <- matrix(nrow=length(shapevec),ncol=length(scalevec))   # initialize storage variable

newparams <- params
for(i in 1:length(shapevec)){
  newparams['shape'] <- shapevec[i]
  for(j in 1:length(scalevec)){
    newparams['scale'] <- scalevec[j]
    likelihood2D[i,j] <- GammaLikelihoodFunction(newparams) 
  }
}

# Visualize the likelihood surface

image(x=shapevec,y=scalevec,z=likelihood2D,zlim=c(1e-70,1e-17),col=topo.colors(12))
contour(x=shapevec,y=scalevec,z=likelihood2D,levels=c(1e-18,1e-17),add=T)

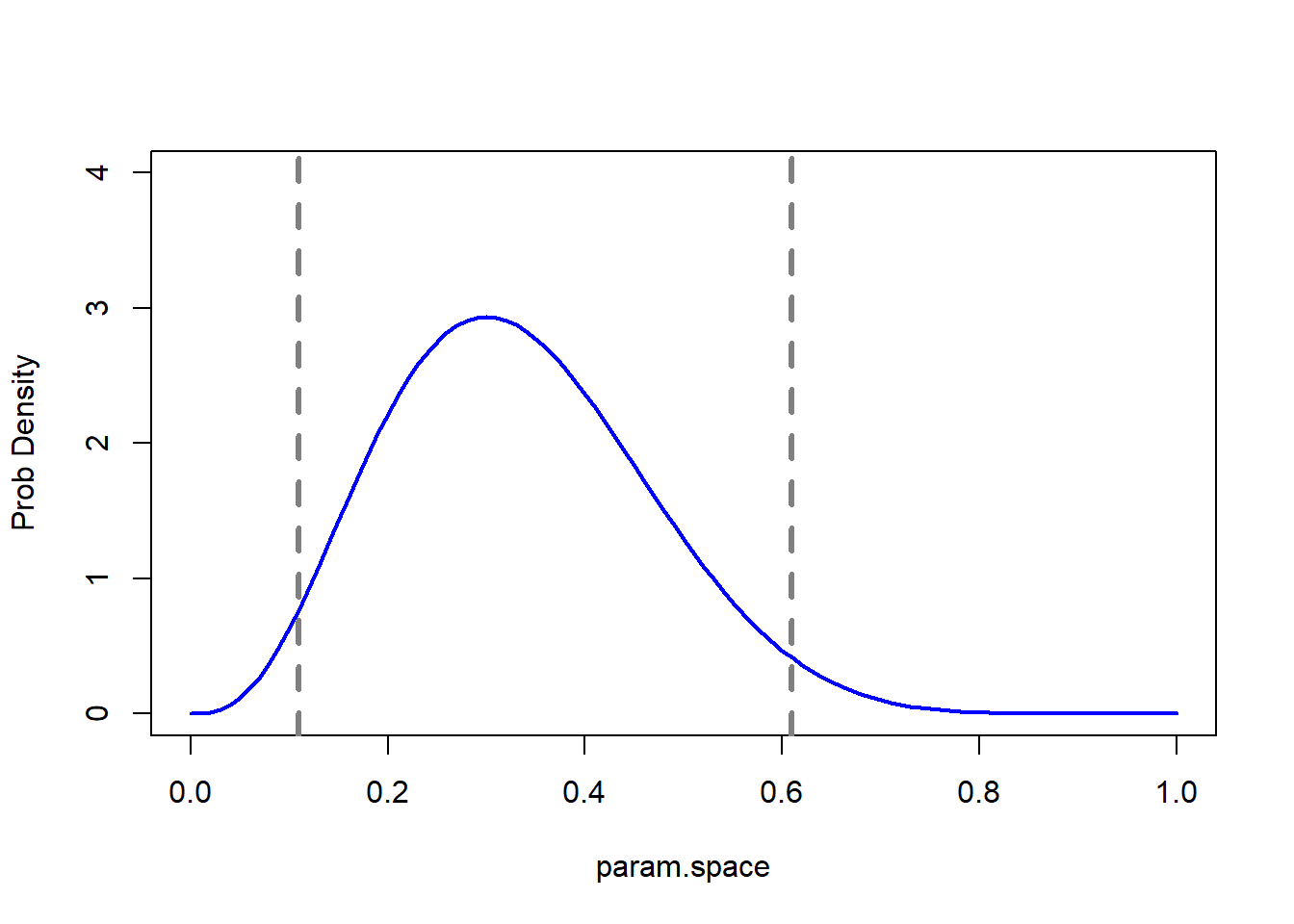
Now let’s use this 2-D likelihood surface as a jumping-off point for a brute-force Bayesian solution to this problem!

First we need to set priors for the shape and scale parameters… For example, we could set uniform distributions for these parameters. For this example, let’s imagine a prior in which all pixels in the above image are equally likely and all pixels outside this range have posterior probability of zero:

# compute the area of each pixel (for probability density computation)

pixelArea <- 0.0001  # for determining probability densities

# define the prior probability surface across this grid within parameter space

prior2D <- matrix(1, nrow=length(shapevec),ncol=length(scalevec))   # initialize prior
prior2D <- prior2D/length(prior2D)

# Visualize the 2-D prior distribution

image(x=shapevec,y=scalevec,z=prior2D,zlim=c(0,0.001),col=rainbow(10))

Okay, not very interesting!

But now we have the raw information we need to apply Bayes’ rule!

# Apply Bayes Rule!   -------------------

weighted.likelihood <- prior2D * likelihood2D    # numerator of Bayes rule
normalization.constant <- sum(weighted.likelihood)    # denominator of Bayes rule

posterior2D <- weighted.likelihood/normalization.constant

# Visualize the 2-D posterior distribution

image(x=shapevec,y=scalevec,z=(posterior2D/pixelArea),zlim=c(0,5),col=topo.colors(12))
contour(x=shapevec,y=scalevec,z=(posterior2D/pixelArea),levels=c(1:4),add=T,drawlabels=FALSE)

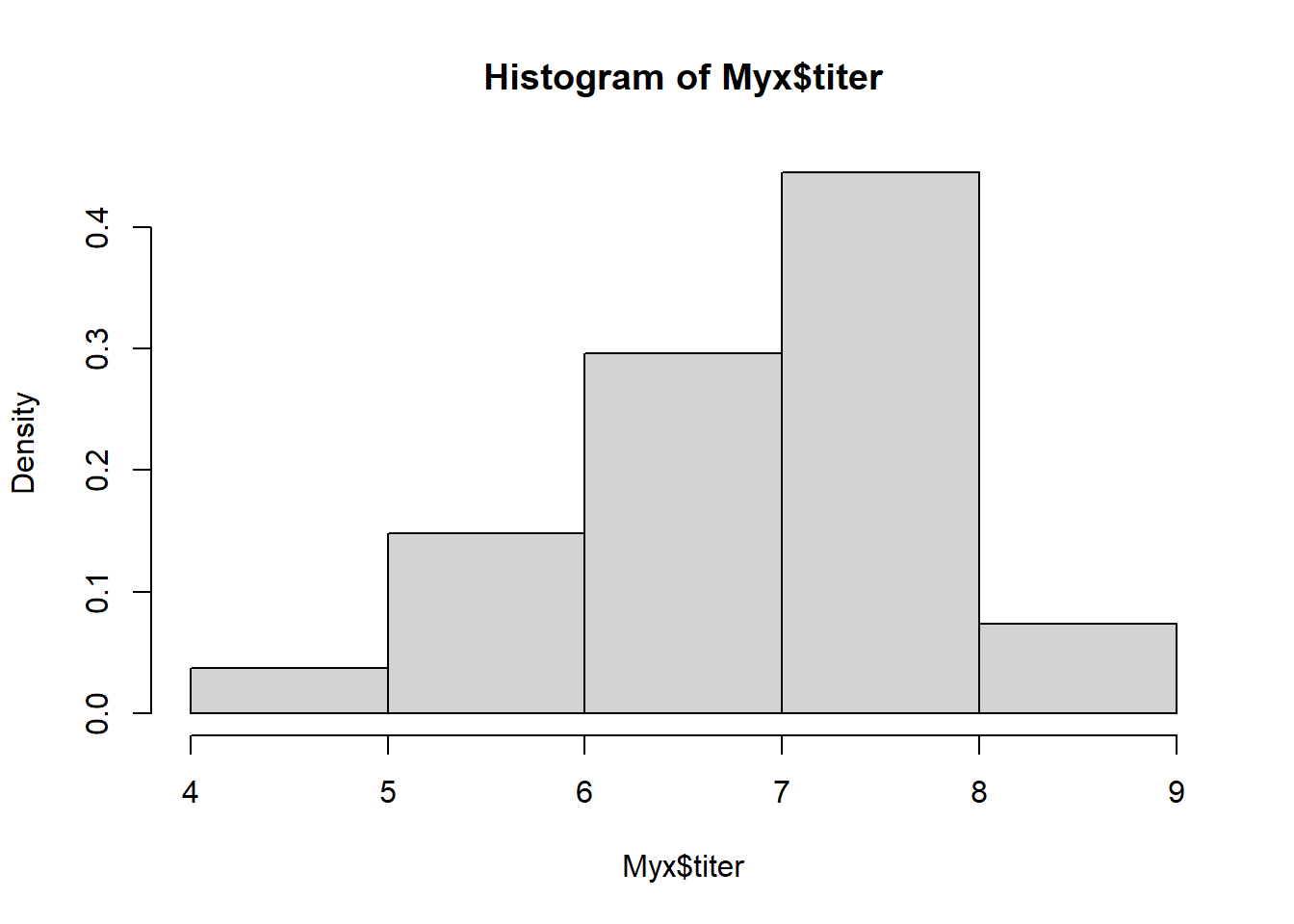
Now we can use this posterior distribution to get our point estimates and parameter uncertainty estimates. We could just take the 2d posterior distribution surface and draw the contour containing 95% of the probability density:

First let’s find the contour line below which only 5% of the probability density is contained (this represents an HPD credible interval):

# try to find the contour that contains 95% of our degree of belief!  ----------------

possible.contours <- data.frame(contour = seq(0.13e-4,1e-4,length=100), quantile = NA)
i=1
for(i in 1:nrow(possible.contours)){
  ndx <- which(posterior2D<possible.contours$contour[i],arr.ind = T)
  possible.contours$quantile[i] <- sum(posterior2D[ndx])
}

head(possible.contours,10)
##         contour   quantile
## 1  1.300000e-05 0.03484278
## 2  1.387879e-05 0.03803099
## 3  1.475758e-05 0.04110702
## 4  1.563636e-05 0.04417352
## 5  1.651515e-05 0.04751733
## 6  1.739394e-05 0.05046922
## 7  1.827273e-05 0.05369474
## 8  1.915152e-05 0.05674380
## 9  2.003030e-05 0.05980036
## 10 2.090909e-05 0.06315809

From here we can see that the contour line at posterior probability 1.739394e-05 encloses ~95% of the probability density

# Visualize the 2D credible region (HPD)

q95 <- 1.739394e-05
image(x=shapevec,y=scalevec,z=posterior2D,zlim=c(0.5e-11,5e-4),col=topo.colors(12))
contour(x=shapevec,y=scalevec,z=posterior2D,levels=q95,add=T,lwd=3,col="red",drawlabels=FALSE)

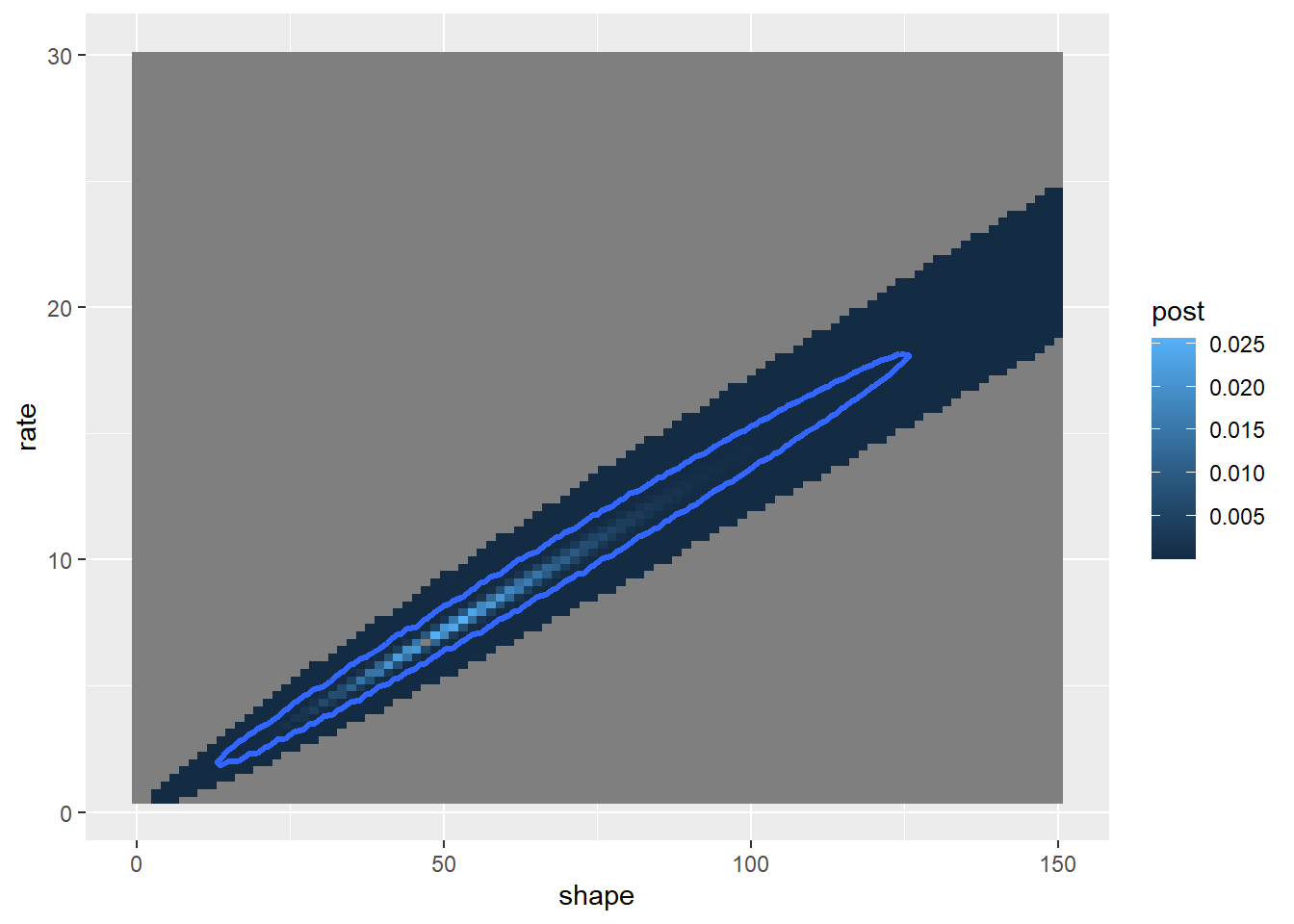
Where is our point estimate? Let’s find the posterior mean and mode!

# Visualize a point estimate

image(x=shapevec,y=scalevec,z=posterior2D,zlim=c(0.5e-11,5e-4),col=topo.colors(12))
contour(x=shapevec,y=scalevec,z=posterior2D,levels=q95,add=T,lwd=3,col="red",drawlabels=FALSE)

meanshape <- sum(shapevec*posterior2D) 
meanscale <- sum(scalevec*posterior2D)
points(meanshape,meanscale,pch=20,cex=2,col="red")  # posterior mean

mode <- which(posterior2D==max(posterior2D),arr.ind = T)
points(shapevec[mode[1]],scalevec[mode[2]], pch="X",col="black",cex=1.5)  # posterior mode

We can also plot out the marginal posterior distributions for the parameters separately. For example, the probability that the ‘shape’ parameter falls within a given range, regardless of the other variable:

# Plot out posterior distributions separately for each parameter  -------------

marginal.dist.shape <- apply(posterior2D,1,mean)     # factor out the scale param- focus only on the shape param.
plot(shapevec,(marginal.dist.shape/sum(marginal.dist.shape))/0.1,type="l",lwd=2,col="blue",ylab="probability density",main="Posterior probability")
abline(v=meanshape)

marginal.dist.scale <- apply(posterior2D,2,mean)
plot(scalevec,(marginal.dist.scale/sum(marginal.dist.scale))/0.001,type="l",lwd=2,col="blue",ylab="probability density",main="Posterior probability")
abline(v=meanscale)

meanshape
## [1] 48.08924
meanscale
## [1] 0.1549478

And from here we can compute the posterior mean and Bayesian credible intervals.

How do our Bayesian estimates compare with the maximum likelihood estimates?? (shape = 49.3666607 scale = 0.1402629)

We can also sample directly from this 2-D posterior distribution:

# Sample parameters from the joint posterior

SampleFromPosterior <- function(n){
  shape <- rep(shapevec,times=length(scalevec))
  scale <- rep(scalevec,each=length(shapevec))
  jointparams <- data.frame(shape=shape,scale=scale)
  probs <- as.vector(posterior2D)
  samples <- sample(c(1:length(probs)),size=n,replace=TRUE,prob=probs)
  jointparams[samples,]
}

samples<-SampleFromPosterior(n=10000)
par(mfrow=c(3,2))
plot(samples,col=1:10000)
plot(samples,type="l")
plot(ts(samples[,1]),xlab="sample",ylab="shape")
plot(ts(samples[,2]),xlab="sample",ylab="scale")
hist(samples[,1],40,xlab="shape",main="histogram of shape param")
hist(samples[,2],40,xlab="scale",main="histogram of scale para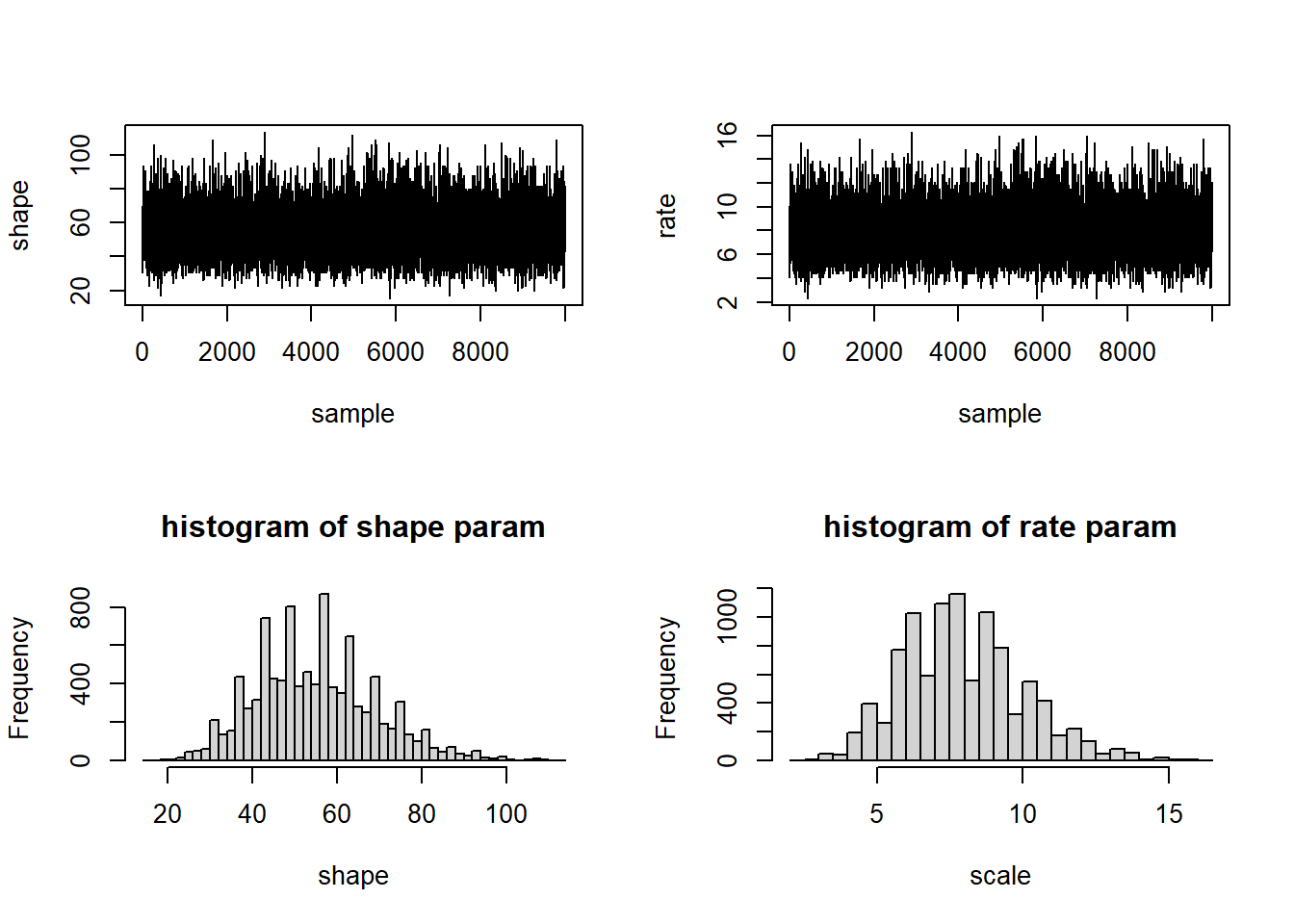m")

par(mfrow=c(1,1))

Markov Chain Monte Carlo

Now in 99% of analysis we will undertake in the real world, we simply won’t have the computational power to partition our parameter space into tiny discrete pixels and completely evaluate the posterior probability for all pixels in that n-dimensional space. In these cases, we tend to harness algorithms known as Markov-Chain Monte Carlo (MCMC). This is the focus of the next lecture.

–go to next lecture–