You can load up the lab script here

Lecture Review

In last week’s lecture, we covered the basics of ordination. We reviewed a bit of matrix algebra, learned to compute the most common distance metrics (Euclidean and Bray-Curtis), and covered unconstrained and constrained ordination techniques.

As a reminder, unconstrained ordination methods do not require any prior knowledge or assumptions about the data, and they are primarily used for visualization. These methods include PCA, PCoA, CA, and NMDS.

In contrast, constrained ordination methods do require prior knowledge and/or assumptions about the data. Constrained ordination methods combine concepts from ordination and regression to test hypotheses. These methods include RDA and CCA.

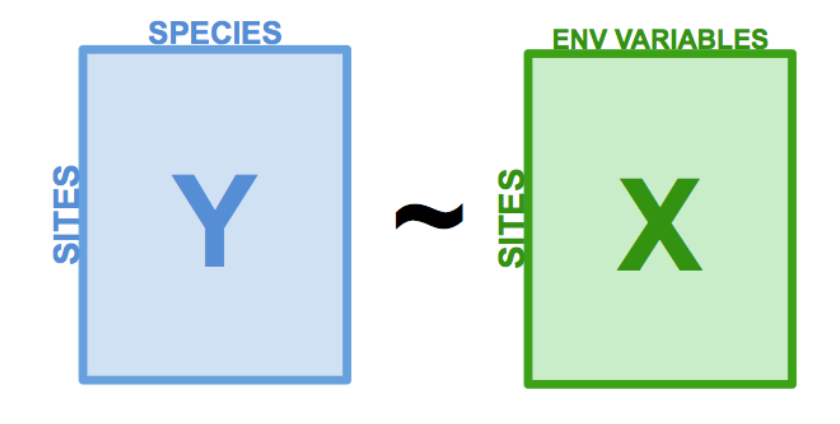
What do we mean by prior knowledge or assumptions about the data? Typically in constrained ordination, we are trying to identify the relationships between a matrix of response variables and a matrix of predictor variables. We partition the variation within the response variables into two parts: the part that can be explained by predictor variables, and the part that cannot be explained by predictor variables. The variation from the response variables that can be explained by the predictor variables is used to create our constrained ordination axes. These axes are constrained by the response variables.

RDA Review

The basic steps of redundancy analysis (RDA) are:

  1. Regress each response variable in y over the predictor variables in x
  2. Perform a PCA on the model predictions

Of course, the actual RDA function from the vegan package is a bit more sophisticated than this. It involves QR decomposition and some complex matrix algebra. But, today we will focus on using RDA, rather than getting into the weeds with matrix math.

Doubs Fish Data

For this example, we will be using the Doubs fish data (Verneaux, 1973). It contains 3 datasets. Doubs.fish is a dataset containing counts of 27 species observed across 30 sites in the Doubs river in France. Doubs.env and Doubs.geo are datasets containing attributes on each site, such as longitude and latitude, slope, pH, and dissolved oxygen concentration.

# Load libraries ----
library(codep)
## Warning: package 'codep' was built under R version 4.3.2
library(vegan)

# Load Doubs fish Data ----
data(Doubs)
species <- as.data.frame(Doubs.fish[-8,])
vars <- as.data.frame(cbind(Doubs.env[-8,],Doubs.geo[-8,]))

Let’s take a closer look at the data, starting with the distribution of abundance values we find.

## Explore the data ----
# Count the number of species frequencies in each abundance class
ab <- table(unlist(species))
# Plot distribution of species frequencies
barplot(ab, xlab = "Abundance class", ylab = "Frequency", col = grey(5:0/5))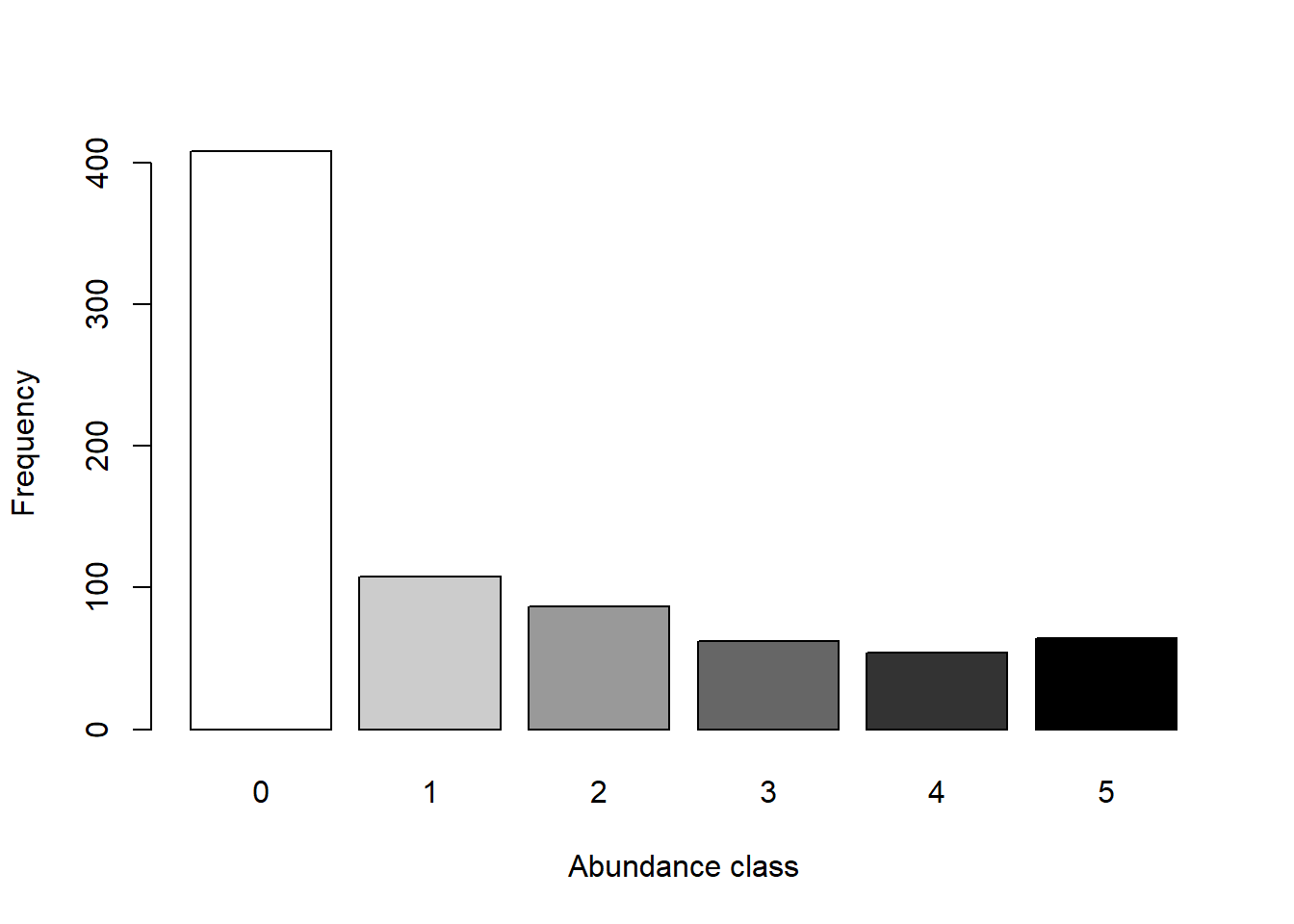

That’s a lot of zeros!

We can also look at the spread of our predictor variables. The help page for the Doubs data gives explanations of what the variables mean.

# Look at the spread of the predictor variables
# ?Doubs
summary(vars)
##       slo              flo              pH             har        
##  Min.   : 0.200   Min.   : 0.84   Min.   :7.700   Min.   : 40.00  
##  1st Qu.: 0.500   1st Qu.: 4.80   1st Qu.:7.900   1st Qu.: 84.00  
##  Median : 1.200   Median :23.00   Median :8.000   Median : 88.00  
##  Mean   : 3.531   Mean   :22.92   Mean   :8.048   Mean   : 85.83  
##  3rd Qu.: 3.000   3rd Qu.:28.80   3rd Qu.:8.100   3rd Qu.: 97.00  
##  Max.   :48.000   Max.   :69.00   Max.   :8.600   Max.   :110.00  
##       pho            nit             amm              oxy        
##  Min.   :0.01   Min.   :0.150   Min.   :0.0000   Min.   : 4.100  
##  1st Qu.:0.10   1st Qu.:0.520   1st Qu.:0.0000   1st Qu.: 8.100  
##  Median :0.30   Median :1.600   Median :0.1000   Median :10.200  
##  Mean   :0.57   Mean   :1.697   Mean   :0.2124   Mean   : 9.472  
##  3rd Qu.:0.58   3rd Qu.:2.500   3rd Qu.:0.2000   3rd Qu.:11.000  
##  Max.   :4.22   Max.   :6.200   Max.   :1.8000   Max.   :12.400  
##       bdo              Lon             Lat             DFS       
##  Min.   : 1.300   Min.   :5.083   Min.   :46.71   Min.   :  0.3  
##  1st Qu.: 2.700   1st Qu.:6.124   1st Qu.:46.90   1st Qu.: 70.5  
##  Median : 4.100   Median :6.338   Median :47.20   Median :185.9  
##  Mean   : 5.014   Mean   :6.359   Mean   :47.13   Mean   :193.0  
##  3rd Qu.: 5.200   3rd Qu.:6.791   3rd Qu.:47.33   3rd Qu.:304.3  
##  Max.   :16.700   Max.   :7.168   Max.   :47.48   Max.   :453.0  
##       Alt       
##  Min.   :172.0  
##  1st Qu.:246.0  
##  Median :375.0  
##  Mean   :470.9  
##  3rd Qu.:752.0  
##  Max.   :934.0

The predictor variables are all in different units, and are on very different scales!

Exercise 1

Before we can perform an RDA, we need to center and scale the predictor variables, as well as account for the double-zero problem. In the previous lecture, we talked about how we can use different distance metrics, such as the Bray-Curtis dissimilarity to account for the double-zero problem. Since we are using the canned RDA function, we don’t have the option to use the Bray-Curtis dissimilarity. The RDA function uses the euclidean distance metric. Therefore, we need to fix the double-zero problem before we feed the data into the RDA function.

We can use the hellinger-transformation to account for the double-zero problem. The hellinger transformation takes raw abundance values, and transforms them into the square root of the relative abundance. The formula for the hellinger transformation is:

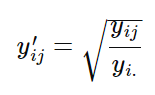
where j represents species and i represents sites (yij represents species j in site i). yi. represents the summed abundance of all species in site i.

Write a function called RDA_prep() that uses the hellinger transformation and the scale function to prepare the data for RDA. This function should be specified as follows:

Input:

Suggested Algorithm:

  1. Using the hellinger formula and a for loop, hellinger-transform the y dataframe. (Hint: convert y to a matrix first).
  2. Use the scale function to center and scale the x dataframe

Return:

You can use the following code to check your answer:

decostand(species, "hellinger")

After you’ve made your function, use it to prepare the Doubs fish data for RDA!

Exercise 2

Now that our data is ready, let’s practice using RDA for variable selection! In real life when we are creating models for inference, we should always select variables based on ecological reasoning. But since none of us work on fish in the Doubs river, and we’re just trying to get some practice using these functions, we’re just going to throw all the data we have at this model!

The ordiR2step() function from the vegan package can help us with variable selection. The concept is similar to the MuMIn::dredge() function. Essentially, it takes a null model and a global model, and then adds predictor variables from the global model to the null model stepwise. If a predictor variable increases the adjusted-R2 value, it keeps it. This works because the adjusted-R2 value calculation contains a penalty for the number of parameters fit, meaning that adding more parameters does not always increase the adjusted-R2.

The two main arguments we need to specify for the ordiR2step() function are object and scope. Object is the null model we want to add to, and scope is the fully specified model we want to pull predictor variables from.

For this exercise, use the rda() function to create null and global models. Then, use the ordiR2step function to choose the best predictor variables. In your word document, answer the following questions:

Exercise 3

So far, we’ve scaled and transformed our data, and used a variable selection tool to narrow down our predictor variables. Say we want to test the hypothesis that our selected predictor variables are impacting the fish community in the Doubs river. There are functions that allow us to obtain R2 and p-values from an RDA!

The RsquareAdj() function extracts the percent of the variation in the response matrix (Doubs fish community) explained by the predictor matrix (environmental variables). This is also called the constrained variance. Then, it adjusts the constrained variance for the number of predictor variables used in the model to obtain the adjusted-R2 value.

The anova.cca() function allows us to test the significance of the predictor variables used in our RDA by implementing an ANOVA-like permutation test. Essentially, if the argument ‘by = “terms”’ is specified, the function will sequentially assess if adding each predictor variable makes a significant difference in the amount of variation explained compared to a null model. It’s important to note that the order of terms will affect their significance, as they are assessed sequentially from first to last.

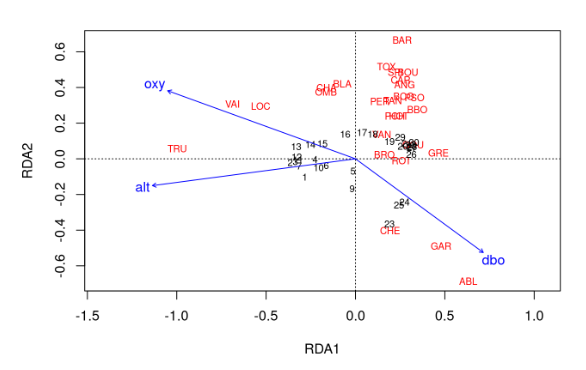
In this last exercise, we will run an RDA on our selected variables, plot the output, and assess its R2 value and significance. After completing these tasks, answer the following questions in your word document: