Intro to population ecology

Central Questions of Population Ecology

Ecological

Why are some species more abundant than others?
What causes population densities to vary in space and time?
What causes populations to go extinct?
What processes regulate population growth?
How can predators and prey coexist sustainably?
What factors allow strong competitors to coexist?
What levels of connectivity are needed to maintain sustainable metapopulations?

Conservation and Management

Is a focal species or population at risk of extinction?
How do modern land use practices affect populations?
What is the Maximum Sustainable Yield for an important game species?
How can insect pests be effectively controlled?
What land (and how much) should be protected to conserve target species?
How can we reduce extinction risk for a focal population while minimizing costs?

What is a population?

From Krebs (1972): “A population is defined as a group of organisms of the same species occupying a particular space at a particular time, with the potential to breed with each other’

Spatial boundaries defining populations sometimes are easily defined, but can also be vague and difficult to determine.

Population size, or abundance, is often represented as \(N\), and is the most basic measurement of a wild population.

Mathematics and Population Ecology

‘Mathematics seems to endow one with a new sense’
- Charles Darwin

‘Like most mathematicians, he takes the hopeful biologist to the edge of the pond, points out that a good swim will help his work, and then pushes him in and leaves him to drown’
- Charles Elton, in reference to a work by Alfred Lotka

‘The importance of the method is this: if we know certain variables, we can predict certain results which would not normally be predictable or even expected by ecologists. The stage of verification of these mathematical predictions has hardly begun; but their importance cannot be under-estimated.’
- Charles Elton

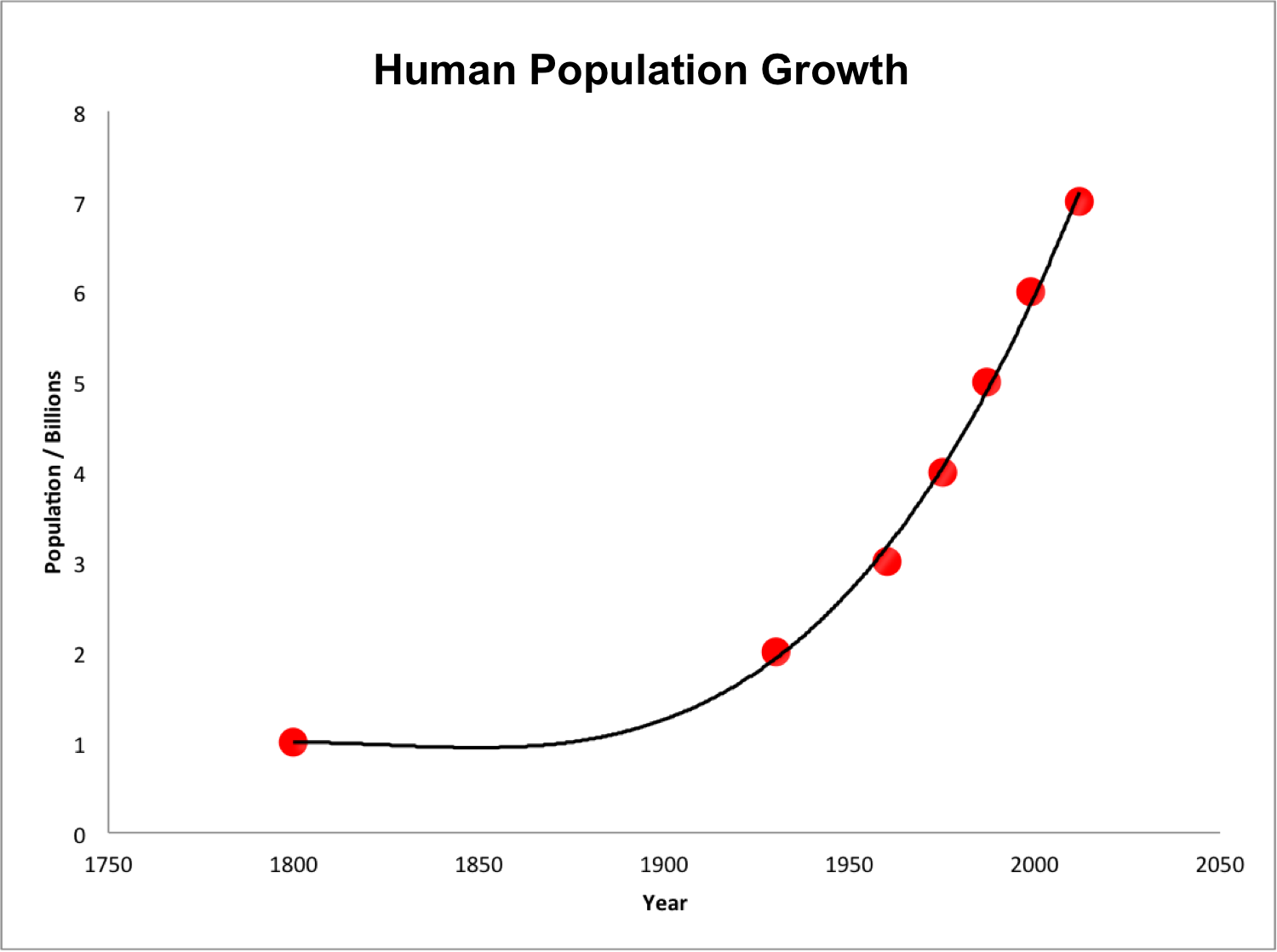
Exponential growth: the fundamental principle of population ecology

Giant puffballs produce 7 trillion offspring (12 zeroes!) in one reproductive event … If all of those individuals reached adulthood, the descendants from just two parent puffballs would weigh more than the entire planet in two generations!

The reason? Populations can exhibit exponential, or multiplicative, growth, in which each each addition to the population expands the rate of population growth (more individuals mean more reproductive output), leading to a positive feedback loop.

Exponential growth is the result of a positive feedback loop.

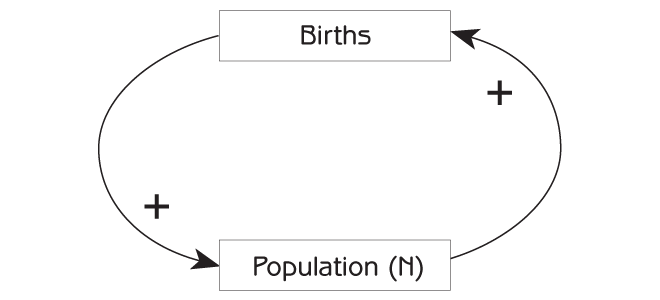
Feedbacks in systems occur when the input and output rates (e.g., births and deaths) vary depending upon the amount in the stock (e.g., a wild population!).

Feedbacks are what leads to complex (‘interesting’) system behaviors and unexpected emergent properties.

A reinforcing, or positive feedback (often called a ‘vicious circle’) leads to exponential growth, leading to insanely high numbers given enough time!

A negative feedback is stabilizing, leading to regulated systems (and homeostasis in organismal biology!). We’ll talk more about negative feedbacks in populations soon enough (population regulation).

In the previous in-class exercise the model structure produced linear growth as the [Flow] added a fixed amount to the [Stock] in each time step.

In-class Exercise: positive feedbacks

Q: What do the following have in common: snowball, people, rabbits, fire, bacteria, fleas, savings accounts, cancer?

Let’s build a model to help us better understand this process.

This model includes a feedback in which the [Flow] rate depends on the amount currently in the [Stock].

Open InsightMaker. Create a [Stock] and a [Flow] as you did in the previous model (flow should be an flow in, not a flow out) and just name them Stock and Flow for now.
If you mouse over Stock or Flow a small [\(=\) Sign] will appear. If you click this it will open the Equation window where you can set values or equations. Open this window for the [Stock], enter a value of 1, then close the window.
Usually there is some type of factor governing the rate the [Stock] influences the [Flow]. Let’s introduce a [Variable] named Rate. To create a [Variable], right-click on the canvas and select Variable from the drop-down. Now draw a [Link] from Rate to the [Flow] (this allows you to use the Rate parameter in the equation for the [Flow]. Open the Equation window for Rate and set it to 0.5.
Open the Equation window for the [Flow] and set it to [Stock] times [Rate]. That is, the total inflow into the [Stock] is equal to the value of the [Stock] multiplied by the value of Rate.
Now click [Run Simulation] and you have just finished your first exponential growth simulation model! Does it do what you would expect?
Think about the first question above while doing this (snowball, people, rabbits, fire, bacteria, fleas, savings accounts, cancer). How would you change the values to represent each of these quantities? Pick a couple of these and try it out!

Q: If [Stock] is a population – say, rabbits – then what is the interpretation of [Flow]? What is the interpretation of Rate? Clone your model, and then Rename your variables accordingly and change the parameters to make the model more biologically realistic for the biological processes they represent. Run the simulation again.

Q Recall the basic equation of exponential growth: \(\Delta N = r \cdot N_t\). How does it relate to the InsightMaker model you have just created? Which component of the equation refers to which component of the model in InsightMaker? [Top Hat]

Q Can you model the puffball example from earlier in the lecture? How many giant puffballs are in the population after two generations?? [Top Hat]

Q Can you (approximately) replicate the human population graph at the beginning of this lecture? What is the per-capita growth rate (\(r\)) of the human population?? [Top Hat] (NOTE: this is totally optional, but you could solve this analytically!)

And just for fun, here is a video about exponential growth you might want to check out..

–go to next lecture–