Passenger Pigeon/Allee effect
NRES 470/670
Spring 2026
Allee Effect

In the last lecture, we talked about how density-dependent feedbacks can regulate population densities over time. In the logistic growth model, we saw that a negative feedback (a decline in population growth rate as density increased) could result in the population stabilizing at its carrying capacity. In population ecology, this type of negative feedback is called ‘negative density dependence’.
What happens if density dependence goes the other way? What if an increase in population density were to induce an increase in population growth rate r? This would be a positive feedback: increased population density results in faster growth, which produces a bigger population, which results in faster population growth, etc.
Imagine a social species, like the prairie dogs pictured above. If the density of prairie dogs is high, they can warn each other about predators. If the density is low, there may not be enough neighbors around to warn each other of approaching danger, and the predation rate might go up, resulting in higher d. This is a positive feedback, and can result in, well, let’s simulate it and find out!
This effect – whereby population growth rate may decrease when population size decreases – is called an Allee effect, named after ecologist Warder Clyde Allee (1885-1955). Allee specialized in social behavior and aggregations, and recognized the benefits of social aggregations to individual fitness.
Interestingly, Dr. Allee’s interest in cooperation and the benefits of social aggregations spilled over into his life in other ways. He was a devout Quaker, an anti-war activist and an advocate of human social cooperation! From the Wikipedia article: “Allee saw ecologists as ‘social healers’ who were able to provide a naturalistic foundation for ethics through their research”

Passenger pigeon
One interesting example of a possible Allee effect involves the extinction of the passenger pigeon (Ectopistes migratorius).

The passenger pigeon was one of the most abundant birds in North America. Some estimate that the total species abundance may have been over three billion at one time!
Aldo Leopold once said,
“Men still live who, in their youth, remember pigeons; trees still live who, in their youth, were shaken by a living wind. But a few decades hence only the oldest oaks will remember, and at long last only the hills will know.” —Aldo Leopold, “On a Monument to the Pigeon”, 1947
What happened to the passenger pigeon?
First of all, pigeons were hunted on a massive scale using wasteful methods.

Secondly, hardwood forests (primary food source for pigeons was mast from hardwood trees) were cleared on a massive scale, reducing available habitat.
But what do passenger pigeons have to do with the Allee effect?
Passenger pigeons were an extremely gregarious (social) species. Once their numbers dwindled (due to hunting and clear-cutting) one hypothesis is that their social systems broke down, and they could no longer effectively reproduce or protect themselves from predators.
In-class exercise: Allee effect
In this exercise we will explore the implications of positive density dependence (Allee effect) on population dynamics.
- In InsightMaker, load up the logistic population growth model with explicit birth and death rate – that is, where \(b\) and \(d\) both decline linearly with increasing population density. It should look something like this (or if you don’t already have this, clone it from here):
It should be structured something like this:
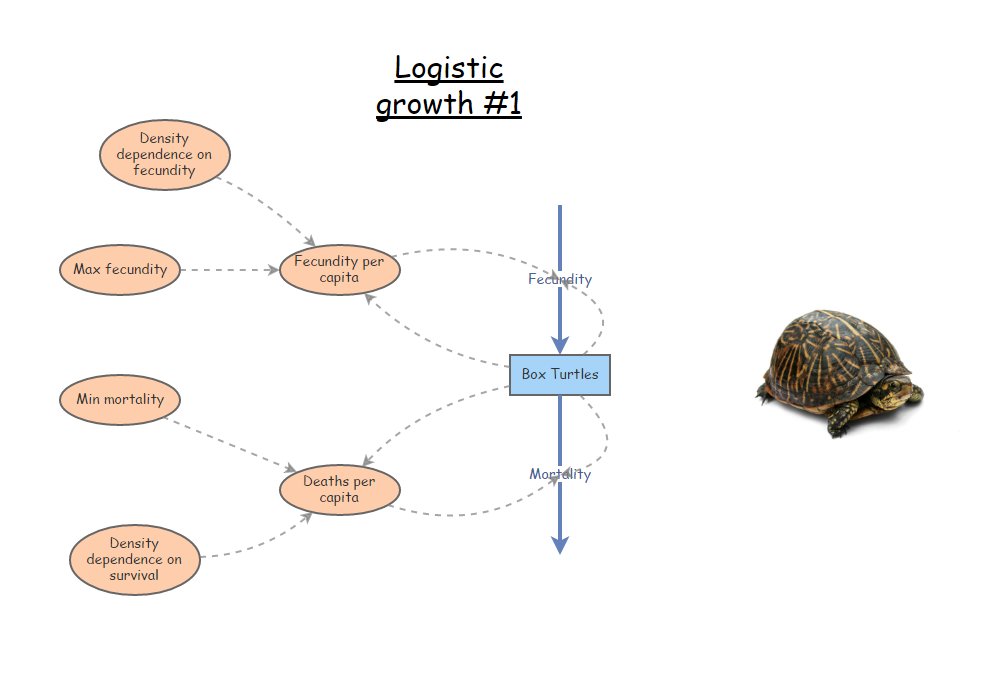
Now add a new [Variable] in InsightMaker called Optimal abundance or Nopt. This is the level of abundance where the population sees all the benefits of social aggregation, yet little of the negative effects of crowding or resource limitation. Set this variable equal to 200 (it is a ‘constant’ and will remain at this value through the simulation).
As for the other parameters, set them as follows:
- Initial abundance: 201 (just above the optimum)
- Density dependence on birth rate: 0.004
- Density dependence on mortality: 0.001
- Max birth rate: 0.8
- Min mortality: 0.3
- Now let’s use a Conditional (IF-THEN-ELSE) statement to specify an Allee effect. The population experiences maximum growth rate at the Allee threshold. If the population is above the optimum, the population exhibits (stabilizing) negative density dependence. If the population is below the Allee threshold, then the population experiences positive density dependence- whereby individuals in smaller populations have lower overall fitness. Positive density dependence can be a destabilizing force if it forces population growth to become negative at low abundances.
To do this, define your Births per Capita using the following syntax (or equivalent):
If [Pigeons]<[Allee threshold] Then
[Max fecundity]-[Density dependence on fecundity]*([Allee threshold]-[Pigeons])
Else
[Max fecundity]-[Density dependence on fecundity]*([Pigeons]-[Allee threshold])
End IfSimilarly, define your Deaths per capita using the following syntax (or equivalent):
If [Pigeons]<[Allee threshold] Then
[Min mortality]+[Density dependence on survival]*([Allee threshold]-[Pigeons])
Else
[Min mortality]+[Density dependence on survival]*([Pigeons]-[Allee threshold])
End IfNOTE: you could accomplish the same task using the absolute value. For example, you could define the per-capita birth rate this way:
[Max fecundity]-[Density dependence on fecundity]*Abs([Pigeons]-[Allee threshold])Think about it- does it make sense that this is the same model?
- If we are running out of time in class, load the model (and clone it!) using this link!
Now you can try to answer the following questions:
Q: What is carrying capacity (K) for this model?
Q: Carrying capacity (K) represents one equilibrium point in this model. Try to find another equilibrium point- that is, a point where the population neither grows nor declines [Top Hat]
Q: is this equilibrium a stable equilibrium or an unstable equilibrium? [Top Hat]
Hopefully it is clear why Allee effects can spell bad news for rare species that were once abundant!
And just for fun, here is some information about the passenger pigeon and its possible “de-extinction”
Q: Do you support Revive and Restore’s efforts to bring back the passenger pigeon? Why or why not??